Background & Motivation

High energy and nuclear physics experiments make use of charged particle beams to accelerate up to 12 GeV and experimentally resolve the fundamental particles that make up the universe. It is then critical to precisely characterize the current density that makes up the charged particle beam.

Contemporary particle detector methods are split into 2 primary categories

1. Fluorescence-Based imaging
2. Direct beam interaction

Fluorescence-based methods use the high energy of the charged particle beam to ionize the detection medium's atoms, where then a camera or scintillator captures the photons released from the relaxation of the atoms. Direct interaction with the particle beam includes methods that treat the particles as an electrical current and by measuring the resulting current across the cross-section of the particle beam, a profile of the charge particles is produced.

These two methods, however, lack in regards to the coherence of the detected photons and in the non-interference of the charged particle beam. In the case of direct particle interaction, a measurement could scatter particles away from the intended target, and decrease valuable transmission of the beam. Whereas in the case of the fluorescence-based detection, the states of the atoms in the detection medium are not well defined, the resulting detection signal is incoherent, and will be incompatible with quantum enhancement methods (squeezed light, inelastic wave mixing, etc.).

Atomic magnetometers and electrometers can be utilized extract the current distribution of the charged particle beam. Since the detector relies on the fields generated by the particle beam, direct particle beam interaction is significantly reduced . Further, as the signal is encoded in a laser resonant to the atoms' transitions, the affected atomic states are well defined, the laser signal is coherent, and can be made more sensitive using methods in quantum optics.

Atomic Magnetometers

Atomic magnetometers are sensitive detectors of magnetic fields, demonstrated to resolve down to tens of femtotesla which is comparable to the magnetic field generated by the human brain. This magnetometer is based on Nonlinear Magneto-Optical Rotation, where the presence of a magnetic field shifts the symmetric ground states of the atom in equal and opposite directions. Tuning a laser to this shifted atomic transition results in the rotation of the laser's linear polarization in the presence of the magnetic field (see Faraday Effect). In short, the rotation occurs due to the birefringent nature of the laser, and where the ground states shift oppositely in the magnetic field, as do the resonances of the left- and right-handed circular polarization components of the laser. Since the linear polarization is a combination of the circular components, the overall polarization of the laser will rotate by an amount linearly proportional the magnetic field experienced by the atoms, demonstrated in (a).

Since we regard the atoms as local probes of the magnetic field, we can image the spatial distribution of the rotated polarization angle. Due to the unique spatial behavior of the magnetic field generated by the electron beam, we can capture the bi-directional magnetic field using this method, as shown in (d):

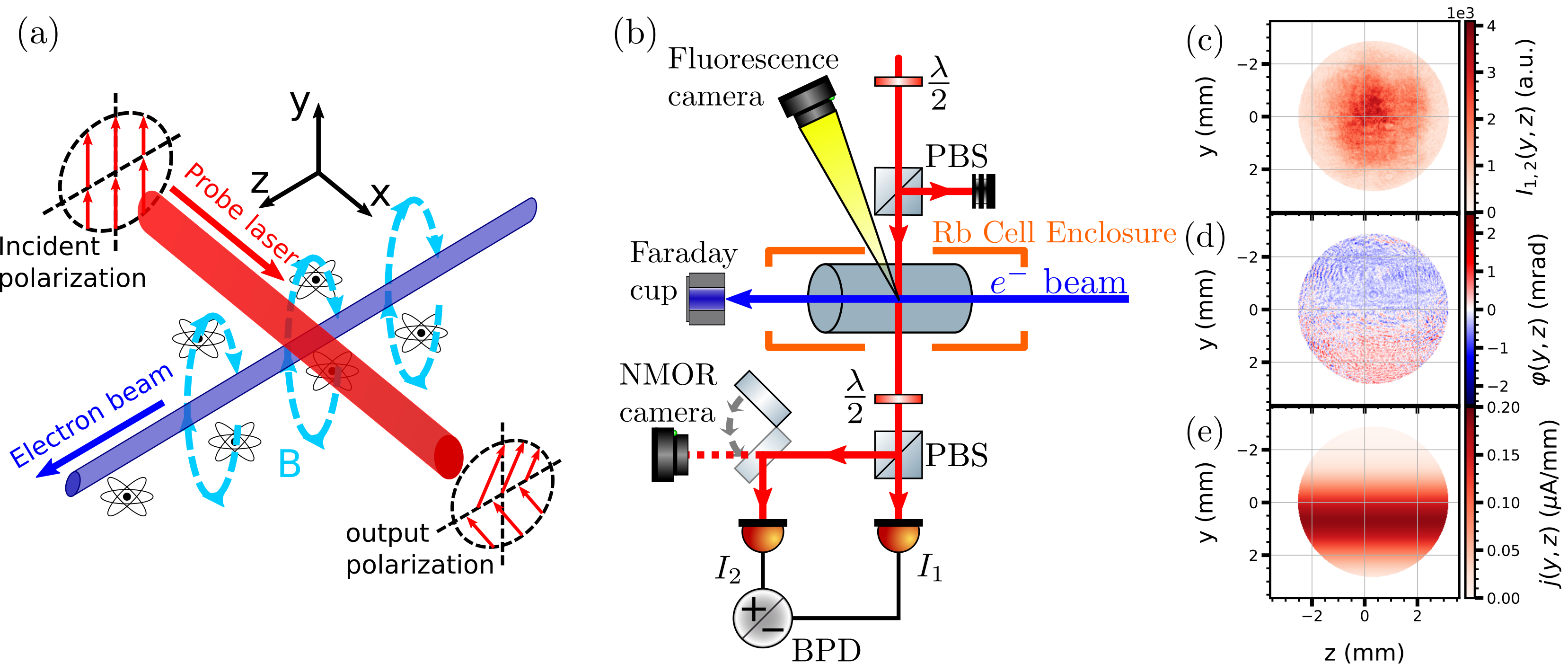
Further, we can derive the vertical current distribution of the particle beam to extract a 2D profile of the particle beam by taking the derivative of the polarization rotation image resulting in the current density profile (shown in (e))

Using these images, we can extract the position, width, and total current of the charged particle beam with a single detector, where contemporary detection systems may include multiple devices to extract the same amount of information on the particle beam. While we don't have an accurate measure of the total loss of the electron beam through this detection medium, the approximate atom density of 10¹² atoms per cm³ is negligible compared to the density of a solid wire of a harp scanner.

While we were able to recover the total current and position of the electron beam by comparing to traditional electron-induced rubidium fluorescence, we cannot accurately recover the total width of the electron beam due to the low intensity (and hence increased noise) on the edges of our probe laser region. Since the width of the electron beam is highly dependent on the shoulders of the polarization rotation profile, uncertainty in these regions will propagate into our estimation of the beam widths. To address this, we are moving toward reducing our noise by using two intensity correlated optical fields to cancel out the common-mode noise of the experiment and improve our detector sensitivity beyond classical limits.

Another potential contribution to the width discrepancy is the contributions of the transverse magnetic fields to our laser propagation direction. In traditional NMOR experiments, the presence of these fields is shown to degrade the sensitivity to parallel magnetic fields. To verify this, we are working on a model to verify the NMOR response in the presence of the full electron beam magnetic field.

We are able to market this detector for relativistic charged particle beams by exploiting the quantum memory, or coherence time, of the atoms. In this case, the atom will recall the passing charged particle long enough for the hardware to capture, and thus renders the accelerating energy of the particle beam irrelevant for beam profiling. To be able to extract the 3D profile of the charged particle beam in 3 dimensions, the detector can be upscaled to include a second probe laser propagating perpendicular to both the existing probe laser and the electron beam. In this case it is possible to extract real-time particle beam diagnostics in 3 dimensions as a tool for high energy particle experiments.

Intensity Squeezing Via Four-Wave Mixing

To address the noise contributions in our detector, we are implementing two optical fields with identical noise characteristics (i.e. intensity fluctuations) through the use of four-wave mixing. Upon subtracting the signals from these two fields, we obtain a signal with noise less than that of a single optical field split and subtracted upon itself! This quantum effect is known as squeezing, where the joint correlations of the two optical fields is stronger than that of the individual fields can be used to optimize the sensitivity of a sensor and in our case, a charged particle beam profiler.

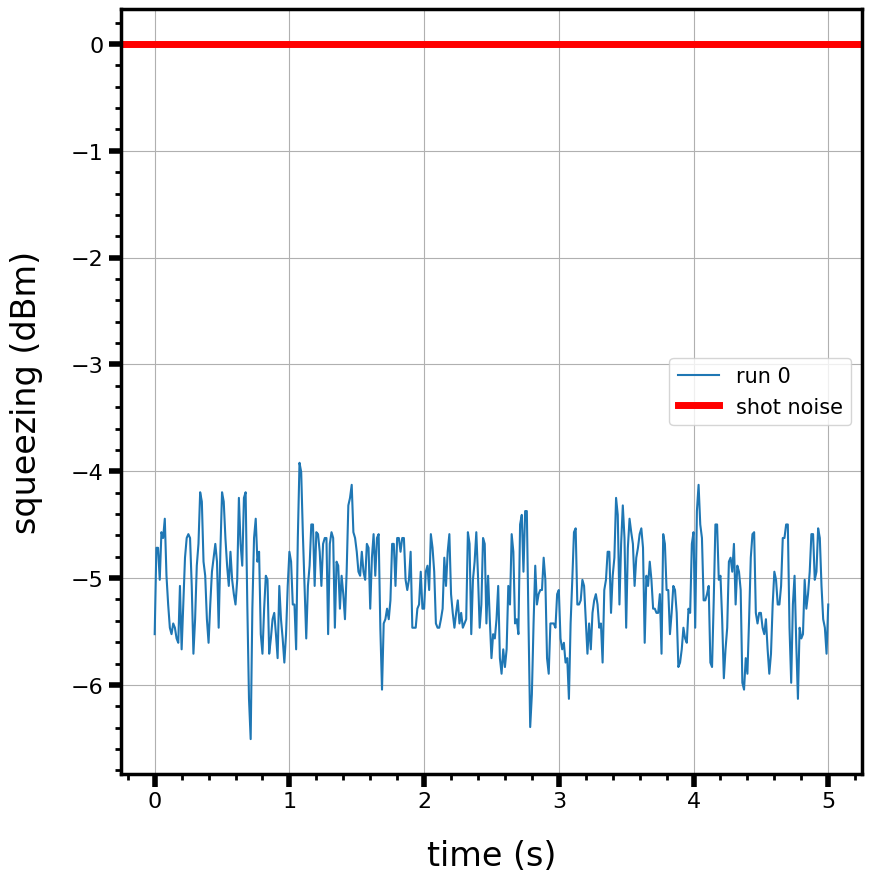
We accomplish two-mode intensity squeezing through four-wave mixing, where a weak-intensity probe and strong-intensity pump laser allow access to nonlinear interactions in the atomic medium. Within this nonlinear interaction, a third field is generated, referred to as the conjugate field, with noise characteristics identical to the incident probe laser. We typically measure the improvement relative to the fundamental noise in the optical field, called the shot noise, based in the intensity of the output probe laser. So far, we have been able to demonstrated -5dB of squeezing, which is equivalent to a factor of 3 reduction of the fundamental optical noise, in addition to common-mode experimental noise reduction.

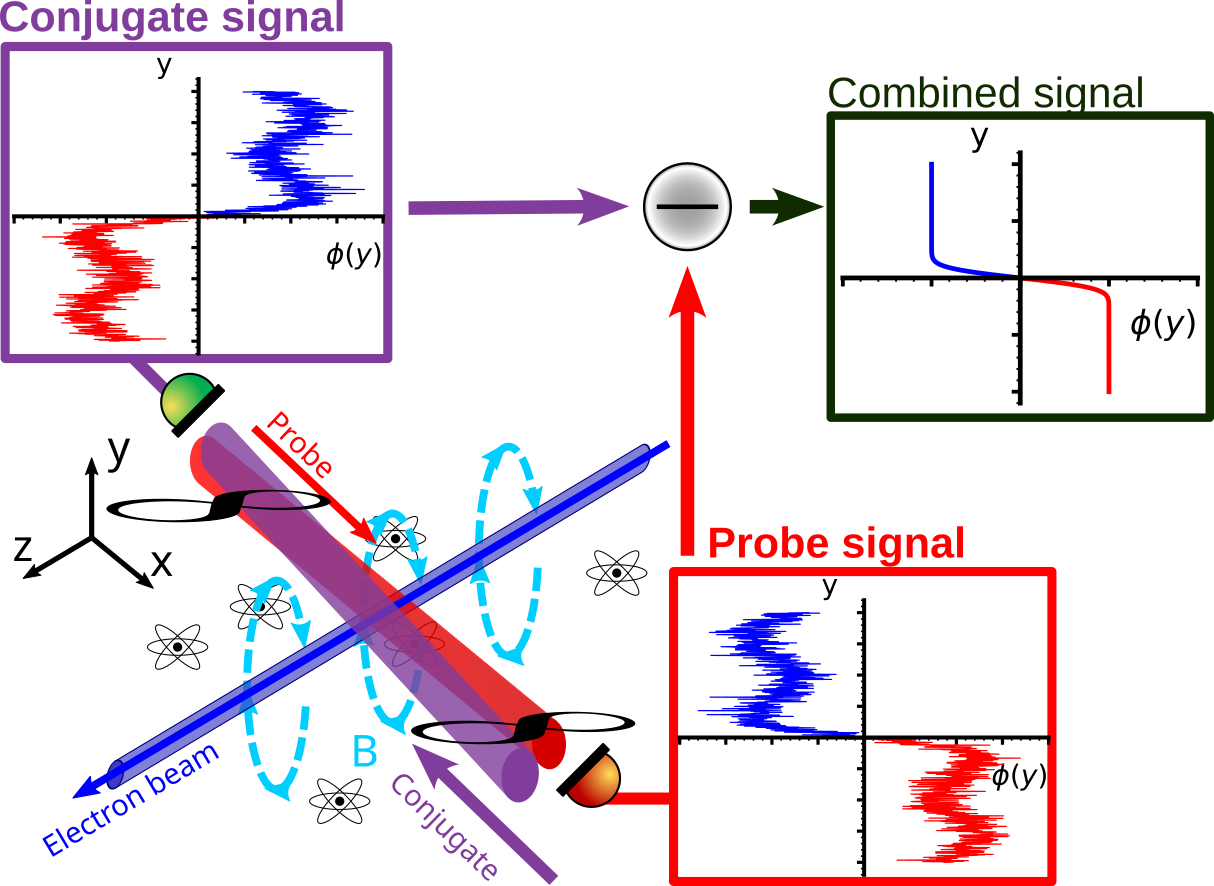
In addition to cancelling the common noises in the experiment, the use of two highly correlated fields can allow us to double our magnetometer signal by considering a counter-propagating configuration. In this scheme, each optical field will experience the opposite polarization rotation direction and upon subtracting the signals from one another, the noise characteristics will vanish and the NMOR signal will double. With this configuration, we can develop a quantum-enhanced tracker for the electron beam to detect extremely low beam currents for a wide range of electron beam energies.