Squeezed Light
Can one squeezed light with atoms?
 Electromagnetic signals are subject to the laws of quantum mechanics. When any optical measurement is made there is thus always noise from quantum fluctuations. This limits many classical measurements to a non-zero noise minimum known as shot noise. However, this barrier can be overcome with quantum techniques, such as squeezed light.
Squeezed light has non-classical statistics that result in noise levels falling below shot noise. As we move into the quantum realm, we begin to deal in uncertainties of measurements rather than absolute known qualities. We project these measurements onto a real and imaginary plane, or onto the quadrature picture, creating a “noiseball” of uncertainty. For classical fields such as coherent or vacuum states the cross sections of the noiseball are equal everywhere. Squeezed states “squeeze” one cross section such that we are more certain of its measurement. Consequently, we "stretch" the opposite cross section resulting in less certainty. The figure shows an example of a non-squeezed noiseball with equal cross-section uncertainty compared to a squeezed noiseball with more certain amplitude (green arrow) and less certain phase (orange arrow) measurements. We produce squeezed light via a process called polarization self-rotation (PSR) in which polarized linear light travels through warm atomic vapor (87Rb).
Electromagnetic signals are subject to the laws of quantum mechanics. When any optical measurement is made there is thus always noise from quantum fluctuations. This limits many classical measurements to a non-zero noise minimum known as shot noise. However, this barrier can be overcome with quantum techniques, such as squeezed light.
Squeezed light has non-classical statistics that result in noise levels falling below shot noise. As we move into the quantum realm, we begin to deal in uncertainties of measurements rather than absolute known qualities. We project these measurements onto a real and imaginary plane, or onto the quadrature picture, creating a “noiseball” of uncertainty. For classical fields such as coherent or vacuum states the cross sections of the noiseball are equal everywhere. Squeezed states “squeeze” one cross section such that we are more certain of its measurement. Consequently, we "stretch" the opposite cross section resulting in less certainty. The figure shows an example of a non-squeezed noiseball with equal cross-section uncertainty compared to a squeezed noiseball with more certain amplitude (green arrow) and less certain phase (orange arrow) measurements. We produce squeezed light via a process called polarization self-rotation (PSR) in which polarized linear light travels through warm atomic vapor (87Rb).
In our experiment, we send linearly polarized laser light, made slightly elliptical by vacuum fluctuations of the horizontal polarization, through a glass cell containing hot 87Rb atoms. This leads to polarization self-rotation as the light propagates, resulting in a squeezed vacuum state of the horizontal polarization at the output of the cell. By mixing this squeezed vacuum field with a strong local oscillator field in a homodyne detection arrangement and sweeping the phase between these fields, we can measure the quadrature fluctuations of the squeezed vacuum. Depending on experimental parameters, we have observed squeezing at several laser frequencies near the Rubidium atomic transitions with our highest level of squeezing to date being about 2 dB of noise suppression.
Classical and Quantum spatial mode reconstruction
 There are significant challenges to characterizing optical fields with low photon counts, such as
the squeezed vacuum. We reconstruct the spatial modes of the electric field to determine the
modes present. This reconstruction method is made up of single pixel imaging (SPI), which
provides amplitude information and homodyne detection, for phase information. SPI calls for
the buildup of an image by spatially modifying the laser beam over a set of structured masks, as
shown in the corresponding image. Obtaining phase information is critical as 3D information
that cameras cannot gather is still available to us.
By combining phase and amplitude information, we can fully reconstruct the wavefront.
There are significant challenges to characterizing optical fields with low photon counts, such as
the squeezed vacuum. We reconstruct the spatial modes of the electric field to determine the
modes present. This reconstruction method is made up of single pixel imaging (SPI), which
provides amplitude information and homodyne detection, for phase information. SPI calls for
the buildup of an image by spatially modifying the laser beam over a set of structured masks, as
shown in the corresponding image. Obtaining phase information is critical as 3D information
that cameras cannot gather is still available to us.
By combining phase and amplitude information, we can fully reconstruct the wavefront.
An example of the image buildup in single pixel imaging to obtain amplitude information as the laser beam is spatially modified over a set of masks. The left image shows the structured masks applied to the laser beam over time. The right image is the buildup of the amplitude information obtained per each measurement. Here we reproduce the letters “P”, “E”, and “R”.
 In the figure we show the reconstruction of several classical objects using our amplitude and phase reconstruction method. Here we use a dried drop of sanitizer (a), a glass plate with sectors of different thickness (b), and a bug wing (c).
The first column of black and white images are references from a traditional camera. The second column shows our phase reconstruction with three-dimensional details that the camera may not be able to gather. The third column shows amplitude reconstruction, which should be similar to the camera reference.
In the figure we show the reconstruction of several classical objects using our amplitude and phase reconstruction method. Here we use a dried drop of sanitizer (a), a glass plate with sectors of different thickness (b), and a bug wing (c).
The first column of black and white images are references from a traditional camera. The second column shows our phase reconstruction with three-dimensional details that the camera may not be able to gather. The third column shows amplitude reconstruction, which should be similar to the camera reference.
 We ultimately use the reconstruction method to image the spatial structures of squeezed light through the measurement of their quadrature noise variance. In our experimental setup, we propose there exists one squeezed mode and one contaminating thermal mode that if strong enough, degrades the squeezing in the system.
By varying the atomic density, we observe different spatial modes at various atomic interaction levels. We test two extreme atomic density cases. The first where we have ideal squeezing and a single circular thermal spatial mode. The second case of higher atomic density permits the thermal mode to overpower any squeezing that may be present and we see a change in spatial mode to two lobe shapes.
We are continuing to update the formalism to more complex cases, such as multi-mode light. The image shows the amplitude reconstructions of thermal modes at different atomic densities. On the left we have a case of ideal squeezing compared to the right where thermal noise dominates.
We ultimately use the reconstruction method to image the spatial structures of squeezed light through the measurement of their quadrature noise variance. In our experimental setup, we propose there exists one squeezed mode and one contaminating thermal mode that if strong enough, degrades the squeezing in the system.
By varying the atomic density, we observe different spatial modes at various atomic interaction levels. We test two extreme atomic density cases. The first where we have ideal squeezing and a single circular thermal spatial mode. The second case of higher atomic density permits the thermal mode to overpower any squeezing that may be present and we see a change in spatial mode to two lobe shapes.
We are continuing to update the formalism to more complex cases, such as multi-mode light. The image shows the amplitude reconstructions of thermal modes at different atomic densities. On the left we have a case of ideal squeezing compared to the right where thermal noise dominates.
Quantum Gaussian states spatial reconstruction
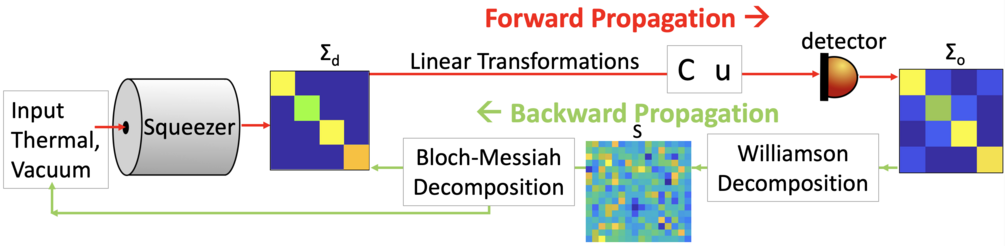
 We developed a way to measure the full covariance matrix of the quantum
Gaussian states in the pixel basis and link it to the spatial profiles of
the generated squeezing modes. The generation of the covariance matrix is
quite labor intensive and requires to do N2 measurements (where
N is number of desired pixels). Once measurement of the covariance matrix
is performed the heavy lifting is done via Williamson and Bloch-Messiah
decomposition.
We developed a way to measure the full covariance matrix of the quantum
Gaussian states in the pixel basis and link it to the spatial profiles of
the generated squeezing modes. The generation of the covariance matrix is
quite labor intensive and requires to do N2 measurements (where
N is number of desired pixels). Once measurement of the covariance matrix
is performed the heavy lifting is done via Williamson and Bloch-Messiah
decomposition.
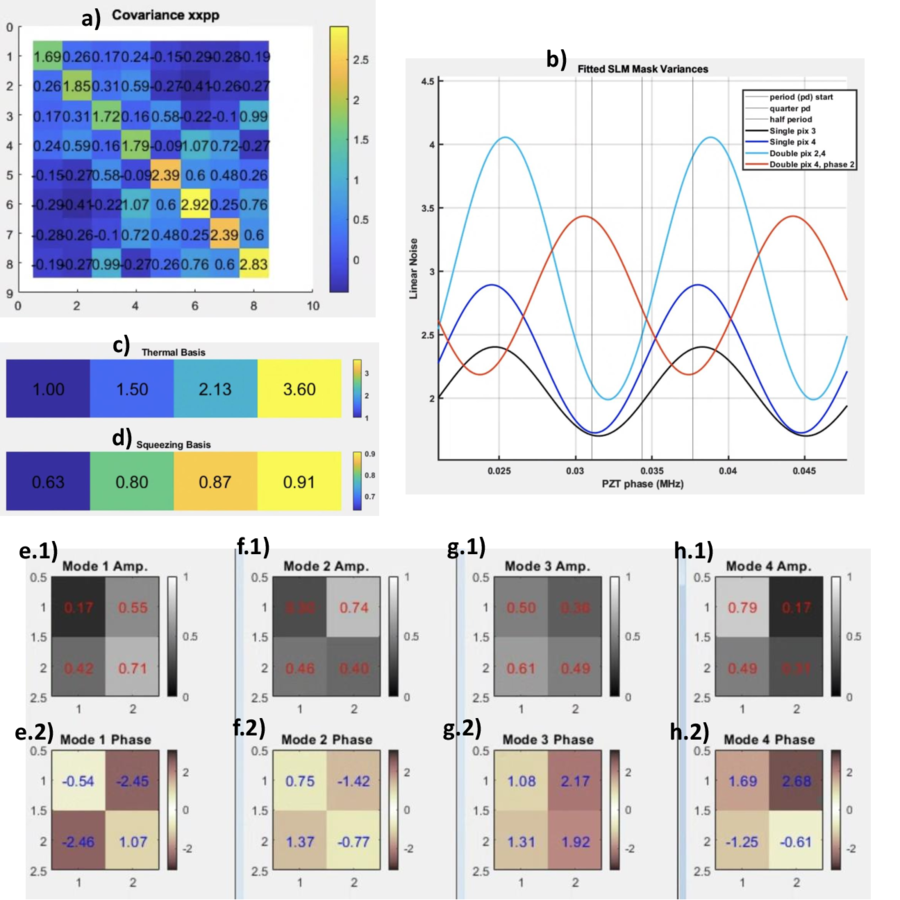
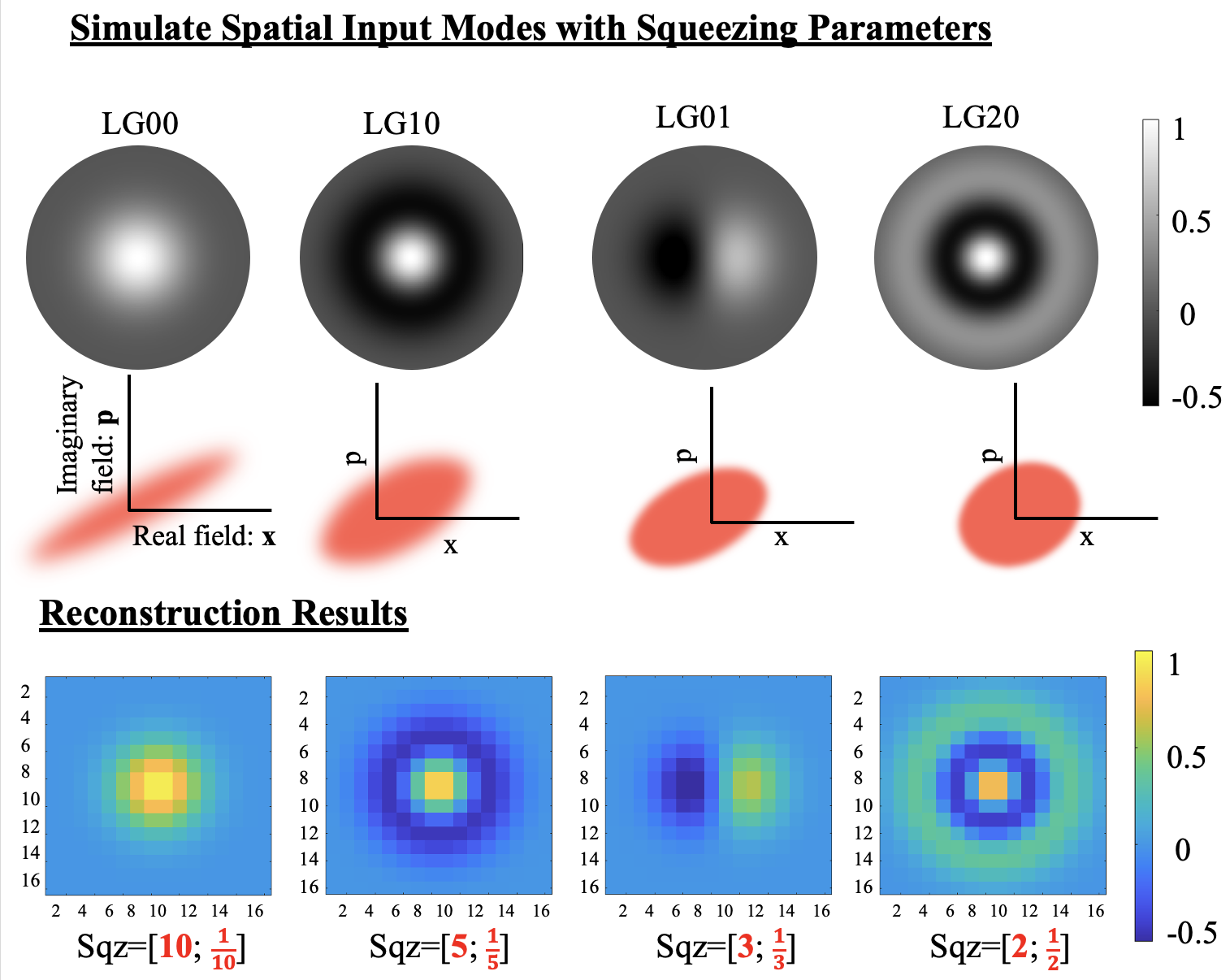 We are also able to simulate a general decomposition method in which no prior assumption of present modes are made. In the associated image, we send in four spatial Laguerre-Gauss modes (LG00,LG10, LG01, LG20) with decreasing squeezing parameters (Sqz=1/10,1/5,1/3,1/2) respectively. By comparing the variance between each axis in the quadrature picture as we rotate the noise ball, we create a full covariance matrix showing how each measurement relates to every other measurement. This matrix is then decomposed first in a thermal mode basis and then in a squeezing mode basis. From this decomposition process we are able to obtain the mode shapes, our four LG modes, and their corresponding squeezing (Sqz=1/10,1/5,1/3,1/2) and anti-squeezing parameters (antiSqz=10,5,3,2). As expected in ideal cases, squeezing is inversely proportional to anti-squeezing.
We are also able to simulate a general decomposition method in which no prior assumption of present modes are made. In the associated image, we send in four spatial Laguerre-Gauss modes (LG00,LG10, LG01, LG20) with decreasing squeezing parameters (Sqz=1/10,1/5,1/3,1/2) respectively. By comparing the variance between each axis in the quadrature picture as we rotate the noise ball, we create a full covariance matrix showing how each measurement relates to every other measurement. This matrix is then decomposed first in a thermal mode basis and then in a squeezing mode basis. From this decomposition process we are able to obtain the mode shapes, our four LG modes, and their corresponding squeezing (Sqz=1/10,1/5,1/3,1/2) and anti-squeezing parameters (antiSqz=10,5,3,2). As expected in ideal cases, squeezing is inversely proportional to anti-squeezing.
Past Projects
Spatial Correlation of Squeezed Quantum Noise
While many experimentally measured characteristics of vacuum squeezing, based on polarization self-rotation in resonant atomic vapor are well described by the existing theory and numerical calculations, there is still a large unpredicted excess noise at higher atomic densities. One possible explanation is a distortion of the squeezing and/or pump field transverse profiles, since it deteriorate the mode matching between the squeezed vacuum field and the local oscillator (pump field).
 To check this hypothesis, we have conducted simultaneous measurements of maximum measured degree of squeezing and the output waist of the laser beam, changing laser power and atomic density. In addition to a regular Gaussian laser beam, we used a first order optical vortex mask, placed before the cell, to produce a Laguerre-Gaussian beam (shown in Fig. 2.1). In this case, the laser beam becomes donut-shaped, with zero intensity in the center. It’s radial intensity distribution can be described by
To check this hypothesis, we have conducted simultaneous measurements of maximum measured degree of squeezing and the output waist of the laser beam, changing laser power and atomic density. In addition to a regular Gaussian laser beam, we used a first order optical vortex mask, placed before the cell, to produce a Laguerre-Gaussian beam (shown in Fig. 2.1). In this case, the laser beam becomes donut-shaped, with zero intensity in the center. It’s radial intensity distribution can be described by ![]()
, where w indicates the beam size. Because of this more complex geometry, we expect the vortex beam to be more sensitive to spatial variations.
 The results of the measurements are shown in Fig. 2.2, and provide some interesting insights. First of all, when the beam was spatially modified, the optimal conditions for generation of maximally squeezed optical field are different: for a Gaussian beam the maximum squeezing was observed at lower pump power and somewhat higher temperature. At the same time, both laser beam profiles showed similar trend in increasing size with atomic density. Such behavior seemed to be largely independent of laser intensity. Such behavior is a strong indication of the linear optics phenomenon, and thus it is unlikely that this self-defocusing affected two orthogonal optical fields differently, ruling out such mode mismatch as the main origin of the increasing quantum noise at high optical densities.
The results of the measurements are shown in Fig. 2.2, and provide some interesting insights. First of all, when the beam was spatially modified, the optimal conditions for generation of maximally squeezed optical field are different: for a Gaussian beam the maximum squeezing was observed at lower pump power and somewhat higher temperature. At the same time, both laser beam profiles showed similar trend in increasing size with atomic density. Such behavior seemed to be largely independent of laser intensity. Such behavior is a strong indication of the linear optics phenomenon, and thus it is unlikely that this self-defocusing affected two orthogonal optical fields differently, ruling out such mode mismatch as the main origin of the increasing quantum noise at high optical densities.
Superluminal squeezing propagation
Classically, an electromagnetic wave can be described with an amplitude and a phase, but on the quantum level it is a flux of photons. This makes it subject to quantum fluctuations – uncertainties in the amplitude and the phase. A typical laboratory laser will produce a beam, which can be closely described as a coherent state of light, a state with minimum uncertainty. Any measurement done on a coherent state will exhibit this minimum uncertainty by having so called shot noise. There are a lot of measurements, where it is the limiting factor. But luckily there is a way to reduce the noise below the shot noise limit.
A coherent state of light has equal uncertainties in the amplitude and the phase. Their product must be equal or greater than the minimum value of 1/4. But there are no limitations on the value of each particular quadrature. So one can, for example, reduce the amplitude noise at the expense of increasing the phase noise. If the uncertainty of one of the quadratures is below that of a coherent state, the state is called squeezed. We study a particular type of squeezed states called vacuum squeezed states, which have zero mean amplitude. For squeezed vacuum states uncertainties in the amplitude and the phase loose their meaning, and we talk about uncertainties in the quadratures X1 and X2.
It is well known, that one can use a resonant media that exhibits anomalous dispersion to produce superluminal classical signals (signals with the group velocity vg>c or vg<0). However, it is not clear from the theoretical point of view, whether it is possible to observe the superluminal propagation of quantum fields. Here we experimentally demonstrate superluminal propagation of a squeezed vacuum state (a quantum field).
 The experimental setup is shown on
Fig. 1. The squeezed vacuum field is generated by shining a horizontally
polarized laser beam with the wavelength of 795 nm into a glass cell, containing
resonant Rubidium atoms. This laser beam is called pump. Because of the
non-linear nature of the squeezing process, we focus the beam using lens L1 to
make a more intense beam inside the squeezing cell. The beam is collimated back
using lens L2. Under the right conditions the coherent vacuum in the vertical
polarization becomes squeezed, and we are able to manipulate its group velocity
in the second cell called interaction cell in Fig. 1. The strong horizontally
polarized pump creates conditions for Faraday rotation in the second cell and
for certain pump powers vertically polarized squeezed vacuum field experiences
anomalous dispersion that leads to superluminal group velocities. We are able
to bypass the interaction cell using two mirrors to determine the reference vg=c . We then detect the squeezed vacuum
using a homodyne detector [9]. The signal is fed into a spectrum analyzer and
recorded on a digital oscilloscope.
The experimental setup is shown on
Fig. 1. The squeezed vacuum field is generated by shining a horizontally
polarized laser beam with the wavelength of 795 nm into a glass cell, containing
resonant Rubidium atoms. This laser beam is called pump. Because of the
non-linear nature of the squeezing process, we focus the beam using lens L1 to
make a more intense beam inside the squeezing cell. The beam is collimated back
using lens L2. Under the right conditions the coherent vacuum in the vertical
polarization becomes squeezed, and we are able to manipulate its group velocity
in the second cell called interaction cell in Fig. 1. The strong horizontally
polarized pump creates conditions for Faraday rotation in the second cell and
for certain pump powers vertically polarized squeezed vacuum field experiences
anomalous dispersion that leads to superluminal group velocities. We are able
to bypass the interaction cell using two mirrors to determine the reference vg=c . We then detect the squeezed vacuum
using a homodyne detector [9]. The signal is fed into a spectrum analyzer and
recorded on a digital oscilloscope.

 I
n order to determine the group
velocity we modulate the level of squeezing by applying a small magnetic field
to the squeezing cell [10]. This degrades the conditions for squeezing
generation and leads to modulation show in Fig. 2. The modulation frequency was 3 kHz.
We then fit the traces and
determine the relative phase between the bypass channel and the interaction
channel. This gives us the possibility to calculate the time difference Δ T between the signals arrival time. Values
that are bigger than zero indicate a delay, while values that are less than
zero indicate advancement. Our result for different pump powers is presented in
Fig. 3.
I
n order to determine the group
velocity we modulate the level of squeezing by applying a small magnetic field
to the squeezing cell [10]. This degrades the conditions for squeezing
generation and leads to modulation show in Fig. 2. The modulation frequency was 3 kHz.
We then fit the traces and
determine the relative phase between the bypass channel and the interaction
channel. This gives us the possibility to calculate the time difference Δ T between the signals arrival time. Values
that are bigger than zero indicate a delay, while values that are less than
zero indicate advancement. Our result for different pump powers is presented in
Fig. 3.