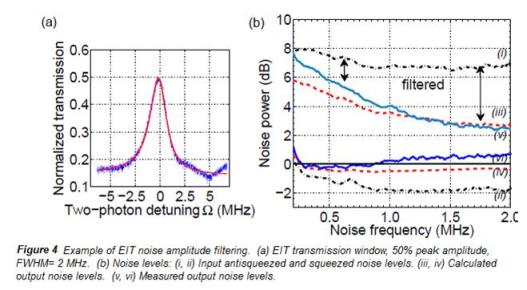
|
Generation of squeezed vacuum in atomic ensembles
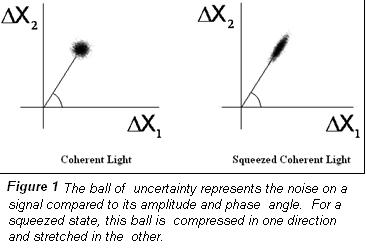
Jump to applications: Any electromagnetic signal is subject to the laws of quantum
mechanics. This means that due to the Heisenberg uncertainty principle, any
optical measurement will have on top of it, noise due to quantum fluctuations,
even if you are measuring the vacuum itself. This limits many measurements to
having a minimum non-zero noise, called shot noise, or the standard quantum
limit.
Squeezed light finds applications in precision measurements
as well as optical communications where the signal to noise needs to be as low
as possible. Due to it's special quantum nature, squeezing may also be applied
in other related areas of quantum optics and quantum information.
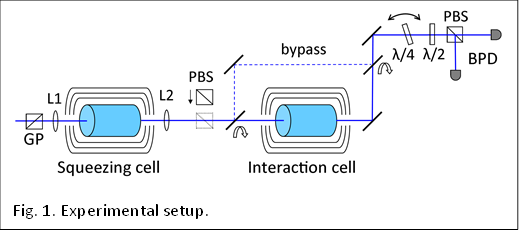
In our experiment,
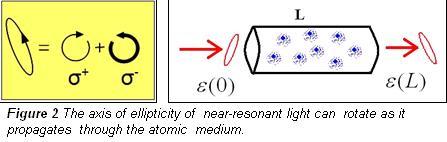
we send linearly polarized laser light, made slightly elliptical by vacuum
fluctuations of the horizontal polarization, through a glass cell containing
hot 87Rb atoms. This leads to polarization self-rotation as the light
propagates, resulting in a squeezed vacuum state of the horizontal polarization
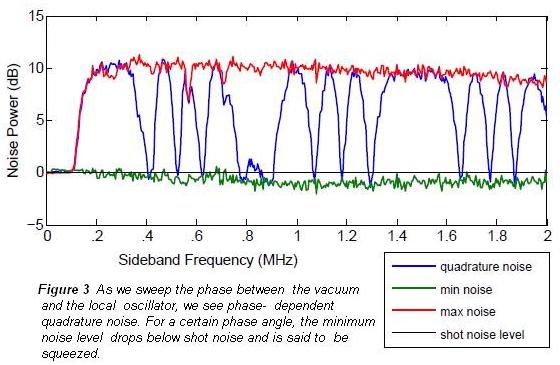
at the output of the cell. By mixing this squeezed vacuum field with a strong
local oscillator field in a homodyne detection arrangement and sweeping the
phase between these fields, we can measure the quadrature fluctuations of the
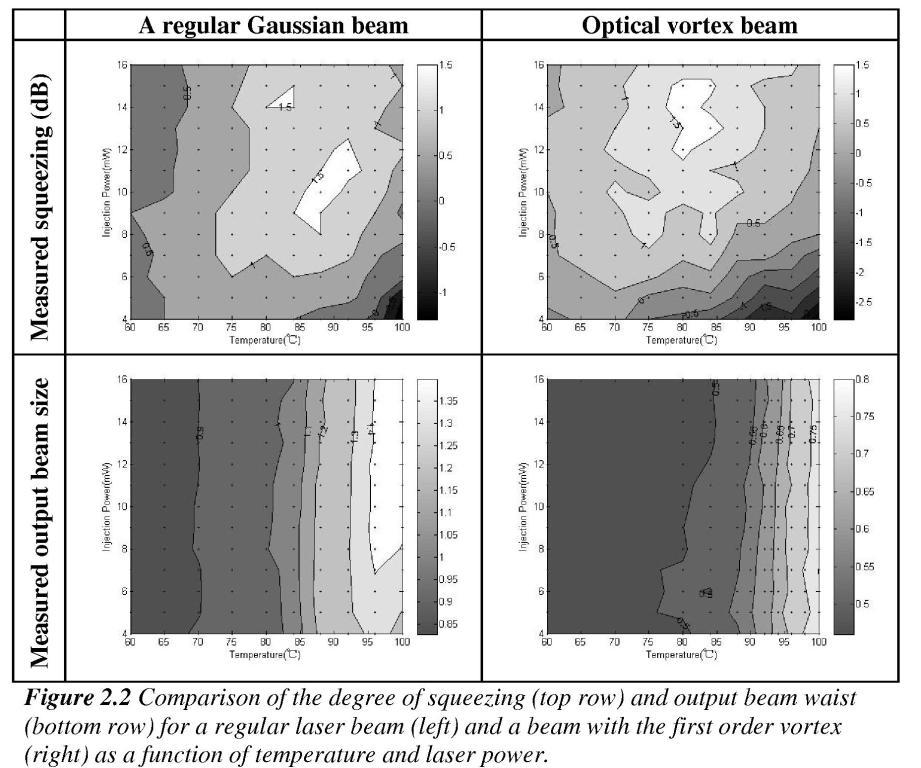
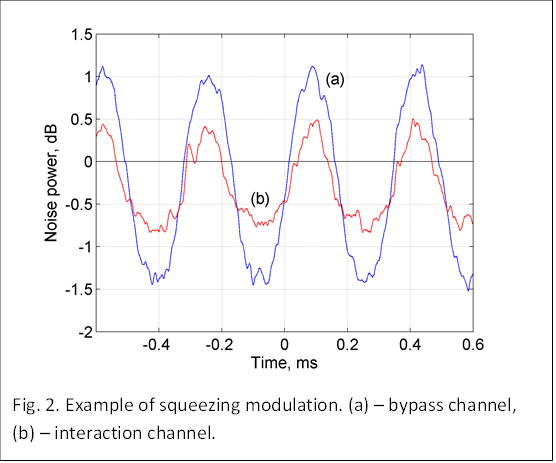
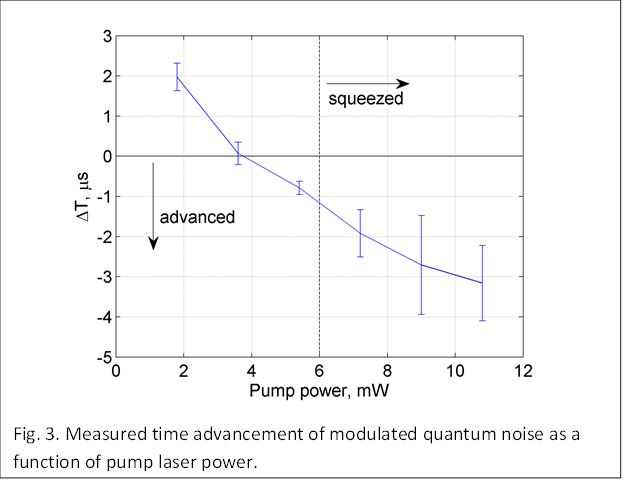
squeezed vacuum. Depending on experimental parameters, we have observed
squeezing at several laser frequencies near the Rubidium atomic transitions
with our highest level of squeezing to date being about 2 dB of noise
suppression. |