Why Matlab

At the very least, it is a great replacement of a hand held calculator. When you need to process multiple data points, it becomes tedious with a simple calculator. Once you master Matlab it will not matter if it is one data point or millions of them. It can do complex math, plotting, fitting, etc. It is also the complete programming language which can stand by itself. Also, Matlab has excellent help documentation and a lot of tutorials at the web.

There are free alternatives. Octave is one example. This is what I personally use instead of Matlab all the time. But it is a bit difficult with installation and it might be scary to see no GUI and only a command prompt for a beginner.

Getting Matlab

Please visit W&M IT software support page and download Matlab from appropriate "Licensed Software >> Math & Statistics Software" section. They have several available versions. Either one is fine. Since we are learning Matlab, we will not have time to go to fancy toolboxes which Matlab provides/removes with new releases.

Statistics functions

Mean of a set

Often you will need to find the mean and standard deviation of a particular sample set. Let's say we estimated a resistor value (R) with different method and obtained the following experimental values.

R

1.20

1.10

1.11

1.05

1.05

1.15

First we transfer it to a Matlab vector variable

R=[ 1.20, 1.10, 1.11, 1.05, 1.05, 1.15 ]

Notice that for a vector variable I use , as a separator.

Now we are ready to calculate mean of this set

mean(R)

with answer 1.1100

Standard deviation of a set

Standard deviation normalized with N-1 samples (so called unbiased estimator) is done with

std(R)

with answer 0.058310. If you need normalization with N samples do

std(R,1)

with answer 0.053229

In both cases, there are too many significant figures, which is unjustified from a physics point of view. So remember, Matlab just does the math for you, the analysis and presentation of results is on you.

How to make a simple plot

Suppose, during the measurements, we obtain for each current value I a voltage V with some uncertainty dV. Our experimental data is represented in the following table.

I	V	dV
0.1	1.0	0.2
1.0	2.2	0.1
1.8	3.2	0.2
3.3	3.8	0.2
4.0	4.9	0.3

First of all, we need to transfer it to the Matlab column vector variables. Pay attention to the delimiter ; between numbers

I  = [  .1; 1.0; 1.8; 3.3; 4.0 ]
V  = [ 1.0; 2.2; 3.2; 3.8; 4.9 ]
dV = [ 0.2; 0.1; 0.2; 0.2; 0.3 ]

Now we make a simple plot without error bars to get the basic. Note that text after % is considered as a comment and Matlab will disregard it.

figure(1) % all plotting output will go to the particular window
plot(I,V, 'x') 

Easy, is not it? Here we mark our data points with crosses and used an 'x' parameter to specify this. You can do other markers as well.

But every plot must be present with title, proper axes labels and units. Note ' for the string specifiers

title('Dependence of voltage on current')
xlabel('Current (A)')
ylabel('Voltage (V)')

Now our plot is nice and pretty.

Fixing the range of the axes

Have a look at the above plot. We see that one of the axes (y) does not contain the origin point (y=0). Such plots are very common in finances and are designed to fool a reader, but they are generally not acceptable in scientific reports and definitely not in my class unless you have a good reason to do otherwise.

The fix is very easy. Note that we are actually sending a vector [0,5] to the ylim function (for x-axis we need to use xlim function).

ylim([0,5])

Now our plot is good to present

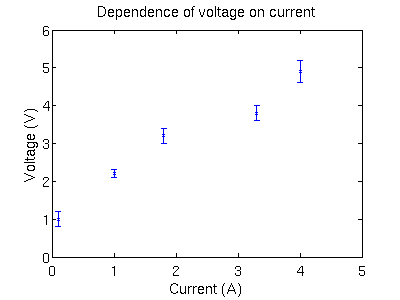
Plotting with error bars

Let's open a new window for the plot

figure(2)

Now we make a plot with error bars, assuming that they are the same for upper and lower parts

errorbar(I,V,dV,'x')
ylim([0,6])

Yet again we need proper labeling

title('Dependence of voltage on current')
xlabel('Current (A)')
ylabel('Voltage (V)')

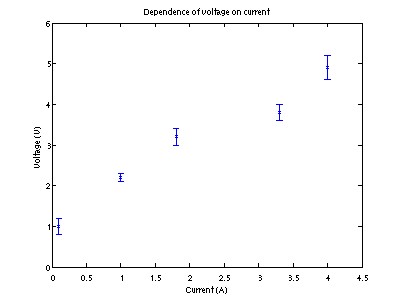
Fixing plots font size

Honestly Matlab is not the best tool to do presentation quality plots, it requires a quite a bit of messing with their GUI. But at least for a quick font size fix do the following. This might look like a magic spell so do read documentation on set command.

fontSize=24;
set(gca,'FontSize',fontSize );

errorbar(I,V,dV,'x')
title('Dependence of voltage on current')
xlabel('Current (A)')
ylabel('Voltage (V)')

Fitting and data reduction

Modern experiments generate a lot of data, while humans can keep in their mind only about 7 things. So there is no way to intelligently work with large data set. We need to extract essential information out of our data i.e. do data reduction. Often we have some idea for analytical representation/model of the experimental data but we are not sure about the model parameters values. The process of extracting them is called fitting.

So let's look at above Voltage vs Current dependence. According to the Ohm's law such dependence must be linear i.e V = R*I. Where R is constant coefficient called resistance.

So first we need to define the model for Matlab. We must specify an independent variable name unless it is called x, which is not our choice here. Also, notice that fittype function wants to know independent variable name thus I is surrounded by ' '

f=fittype( @(R,I) R*I, 'independent', 'I' )
%______________^ independent variable must be last in the function arguments
%____________^ even though R is supposed to be fixed it is still a variable
%              from fitting point of view

Now our job is simple, we need to specify a guessed value of the R as starting point for the fit function.

param_guessed = [ 4 ]

You might have a model with multiple parameters than it is a bit more evolved. Please, do read help file about fitting.

Finally, we fit.

[fitobject, goodness_of_fit] = fit (I, V, f, 'StartPoint', param_guessed)

You will see the following

fitobject = 

     General model:
     fitobject(I) = R*I
     Coefficients (with 95% confidence bounds):
       R =       1.291  (0.8872, 1.695)

goodness_of_fit = 

           sse: 2.6340
       rsquare: 0.7050
           dfe: 4
    adjrsquare: 0.7050
          rmse: 0.8115

The most interesting part is R = 1.291 (0.8872, 1.695), where 1.291 is the mean for the extracted parameter R and (0.8872, 1.695) is the interval within one standard deviation. So we get our error bars as well: one sigma is equal 1.695 - 1.291 = 0.4040

So our conclusion is that R = 1.3 +/- 0.4.

Checking the fitting result

We should not trust computed fit parameters blindly. For our simple case it is probably OK, but for more evolved nonlinear fitting functions result might go way off if we specify starting point significantly far from optimal.

One way to check the fit quality is to look at the Root Mean Squared error (rmse) parameter from the above output. It reflect what is the typical deviation of the model/fit from experimental points. It should be about the size of your experimental error bars. If it is much smaller then most likely you are over fitting (you model has to many free parameters). If it is much bigger your fit model is not good enough.

Another way to check consistency of the fit it to look at plotted data and the fit simultaneously. Let's open yet one more window and plot our data first

figure(3)
fontSize=24;
set(gca,'FontSize',fontSize );

errorbar(I,V,dV, 'x')

hold on

Notice the hold on statement. With it, the next plotting command draws over the already presented plot, i.e. graphics window holds on to its content. Note, that the default behavior is to make a brand new plot with every graphic related command.

Now, we make the plot corresponding to our model/fit. There are multiple way to do it, the simplest is

plot( fitobject )

title('Dependence of voltage on current')
xlabel('Current (A)')
ylabel('Voltage (V)')

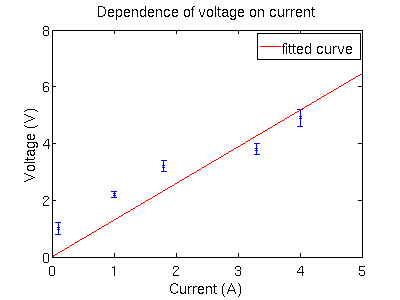
This is not a very good fit since the fit line is more than a typical experimental error away most of the time.

More elaborated fit

It looks like our voltage has some offset. We need to update our model to include Vb the biasing voltage term: V = R*I +Vb. So our fit/model should include two unknown parameters: R and +Vb

f=fittype( @(R, Vb, I) R*I+Vb, 'independent', 'I' )

We need to provide initial guess for two parameters

param_guessed = [ 4, .5 ]
%_________________^           R value
%____________________^^       Vb value

The rest of the procedure is the same as above

[fitobject, goodness_of_fit] = fit (I, V, f, 'StartPoint', param_guessed)

and we see fit parameters R and +Vb below

fitobject = 

     General model:
     fitobject(I) = R*I+Vb
     Coefficients (with 95% confidence bounds):
       R =      0.9094  (0.5556, 1.263)
       Vb =       1.165  (0.2817, 2.048)

goodness_of_fit = 

           sse: 0.3832
       rsquare: 0.9571
           dfe: 3
    adjrsquare: 0.9428
          rmse: 0.3574

Let's see how our new fit looks like

h=figure(4); % this handle 'h' will be useful for saving figure
fontSize=24;
set(gca,'FontSize',fontSize );

errorbar(I,V,dV, 'x')
hold on

plot( fitobject )

title('Dependence of voltage on current')
xlabel('Current (A)')
ylabel('Voltage (V)')

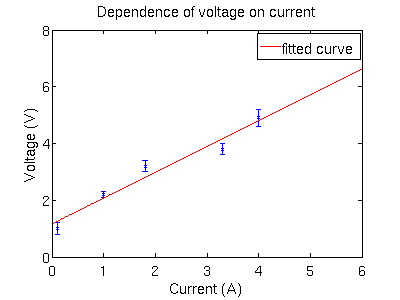
This seems to be a much better fit.

Nonlinear fitting

Suppose we would like to check inverse square law. This is how it can be done.

% Let's build a (fitting) model, i.e. function which would describe our data.
% Note that independent variable should be called x and it is the last.
ft=fittype( @(A,x0,B,x) A./(x-x0).^2 + B); 
% A is a scale coefficient
% x0 is offset along radial direction
% B is the sensor reading due to background

Np=20; % number of test points
r=linspace(.1, 5, Np)'; % radial distance from the object
% Constructing artificial sensor data, note addition of the noise with randn 
s=feval(ft, 1.5, -0.2, 0.2, r) + 0.3*randn(Np,1); % a=1.4, x0=-0.1, B=0.2

figure(2); clf;
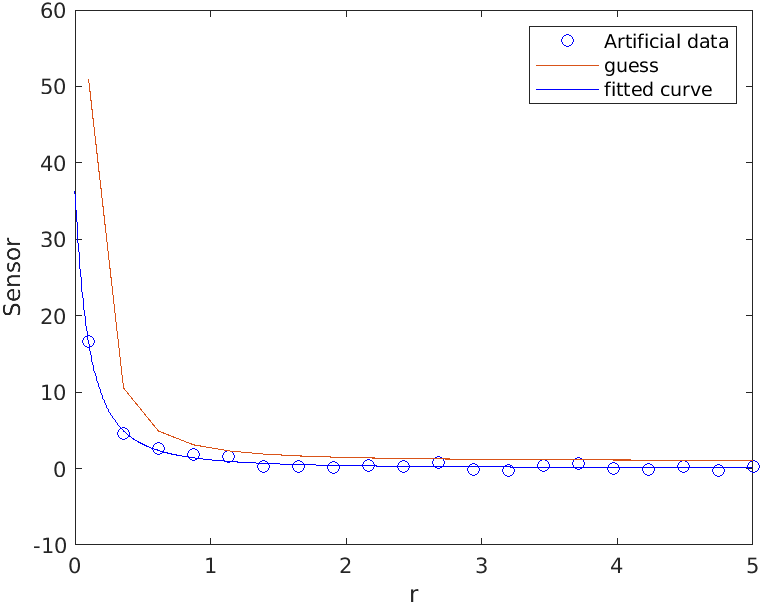
plot(r,s,'bo', 'DisplayName', 'Artificial data');
hold all;
legend;

% Note that is good idea to provide a guess values for our A, x0, and B parameters
% Below A=2, x0=-0.1, and B=1. The fit is most sensitive to x0 values
% it is good idea to manually tune such parameters to see how good is a guess execute
plot(r, feval(ft, 2, -0.1, 1, r), 'DisplayName', 'guess' )

% once we are happy with initial guess, we are ready to fit
[fo, go] = fit(r,s,ft, 'StartPoint', [2,-0.1,1])

plot(fo, 'b-'); % add the final fit curve to the plot
xlabel('r')
ylabel('Sensor')

The output will look like

fo = 
     General model:
     fo(x) = A./(x-x0).^2+B
     Coefficients (with 95% confidence bounds):
       A =        1.56  (1.077, 2.043)
       x0 =     -0.2078  (-0.2559, -0.1597)
       B =     0.07226  (-0.1422, 0.2868)

go = 
  struct with fields:

           sse: 2.1829
       rsquare: 0.9917
           dfe: 17
    adjrsquare: 0.9908
          rmse: 0.3583

As we can see that fitted parameters are matching the data parameters within their confidence intervals, though the uncertainties are quite large. To improve it we need either less noisy data or more points near x0 where sensor values are the largest.

In the goodness of fit variable (go) the most interesting field is the root mean square error (rmse). For good fit models it should be comparable with uncertainty of the sensor measurements, in our case it was due to fake normally distributed noise with standard deviation of 0.3 which matches quite well the value of rmse=0.3583.

Saving your Matlab plots

Well, it is nice to have Matlab plots. But as soon as you close Matlab they will go away. How to save them for a future use?

Matlab 2020 and later

Use exportgraphics command. It can do several graphics formats. Among them, png and pdf are the most important.

For figure saved in png format do

exportgraphics(h, 'V_vs_I.png')

notice that we are using handle 'h' for the figure which we created before

If we want pdf format

exportgraphics(h, 'V_vs_I.pdf')

unlike older print command below, it will have nicely cropped plot without huge white margins. This file is suitable to be inserted in you document right away.

There are other parameters for exportgraphics which you might find useful.

Prior Matlab 2020

Use print command. Unlike the name suggest it does not make a carbon copy but actually an electronic one.

For figure saved in png format do

print('-dpng', 'V_vs_I.png')

If you find that your figures are too large, specify the resolution in dots per inch with -r option. For example

print('-dpng', '-r50',  'V_vs_I.png')

or if you need a pdf (Matlab usually make very bad pdfs without a lot of tweaking)

print('-dpdf', 'V_vs_I.pdf')

The -d stands for output driver option, i.e png or pdf in above examples.

Make sure that you read documentation for print command there are some useful parameters.

Where to learn more

At W&M Physics 256 class teaches how scientists use computers. Matlab was a language of choice for this class. Feel free to read and use my Physics 256 materials make sure that you read at least Lecture 02 slides. Also lecture 05 slides discuss data reduction and fitting. There is also fitting chapter from my book Programming with MATLAB for Scientists: A Beginner’s Introduction.