a) Given that the length of a year is approximately 365 days, and given that the mass of the sun is 2.0 x 10³⁰ kg, calculate the average distance from the Sun to the Earth.
(G = 6.67 x 10^-11 N m²/kg²)

b) Many years from now, scientists discover that the Sun is about to go nova (i.e. explode in a particularly nasty manner). This would incinerate the Earth. To save the world, physicists will use powerful rockets, mounted on the Earth's surface, to propel the Earth out of the solar system. How fast would the Earth have to be moving in order to escape from the sun's gravitational field? Ignore the effect of all other planets, moons, etc. in the solar system.

a) Here we can apply Kepler's 3rd Law. This arises from equating the gravitational force to the mass times the centripetal acceleration, and uses the fact that the orbital velocity v = (2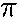R/T) where T is the period. Thus it gives

mv²/R = GmM/R²

m(2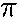R/T)²/R = GmM/R²

or, rearranging,

R³ = T²GM/(4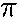²)

where R = Earth-Sun distance, m = mass of Earth. M = mass of Sun, and T = period = one year. Converting the year to units of seconds

T = (365 d)(24 hr/d)(3600 s/hr) = 3.15 x 10⁷ s

Thus we have

R = [(3.15 x 10⁷ s)²(6.67 x 10^-11 N·m²/kg²)(2.0 x 10³⁰ kg)/(4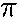²)]^1/3

   = 1.50 x 10¹¹ m

b) This is an escape velocity question; choosing the gravitational potential to be zero at infinity, we have U = -GMm/r. For the Earth to escape the solar system, it must be able to have (at least) zero speed at infinity, so its total energy must be great than equal to zero, i.e.

W = (1/2)mv² - GmM/r = 0

Plugging in r = R (the Earth-Sun distance) we have

(1/2)mv² - GmM/R = 0

or

v = [2GM/R]^1/2

v = [2(6.67 x 10^-11 N·m²/kg²)(2.0 x 10³⁰ kg)/ 1.50 x 10¹¹ m]^1/2

   = 4.22 x 10⁴ m/s

Next problem
Test 3 page
Physics 101 Home page
Physics Department Home Page