Problem 4:
-
A merry-go-round of radius 2 m is rotating about a frictionless pivot.
It makes one revolution every 5 s. The moment of inertia of the
merry-go-round (about an axis through its center) is
500 kg·m2.
A child of mass 25 kg, originally standing at the exact center, walks out
to the rim. The child can be considered as a point mass.
-
a) What is the new angular velocity of the merry-go-round?
- b) Does the total kinetic energy of the system increase or
decrease? By how much?
- c) Where does this change in kinetic energy go to or come from?
Solution:
- We have no net external torques on the system, so we can apply conservation
of angular momentum. Thus we have
- L = I
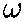 = Inew
= Inew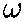 new
new
- or
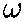 new =
I
new =
I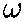 /Inew
/Inew
- The child when at the center of the merry-go-round contributes nothing to the moment of
inertia, but when she is at the rim she contributes
- Ichild = mchildR2
- Thus we have
- I = 500 kg·m2
- Inew = 500 kg·m2 + (25 kg)(2 m)2
- = 600 kg·m2
- Converting the units of
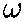 :
: -
-
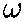 = [1 rev/(5 s)](2
= [1 rev/(5 s)](2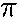 rad/rev)
= (2/5)
rad/rev)
= (2/5)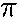 rad/s
rad/s
- Therefore
-
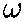 new = [(500 kg·m2)/(600
kg·m2)]( (2/5)
new = [(500 kg·m2)/(600
kg·m2)]( (2/5)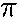 rad/s)
rad/s)
- =
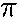 /3 rad/s
= 1.047 rad/s
/3 rad/s
= 1.047 rad/s
- b) Rotational kinetic energy:
- K = (1/2)I
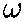 2
= (1/2)(500 kg·m2)((2/5)
2
= (1/2)(500 kg·m2)((2/5)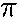 rad/s)2
= 395 J
rad/s)2
= 395 J
- Knew = (1/2)Inew
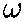 new2
= (1/2)(600 kg·m2)((1/3)
new2
= (1/2)(600 kg·m2)((1/3)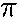 rad/s)2
= 329 J
rad/s)2
= 329 J
- Thus the energy decreases by 395 J = 329 J =
66 J
.
- c) The loss is energy is due to work done by friction between the
child's feet and the surface of the platform. If there was no friction, the child would
slip as the merry-go-round rotates under her feet. The child's muscle's end
up dissipating most of the energy as heat.
Test 3 page
Physics 101 Home page
Physics Department Home Page
College of William and Mary,
Dept. of Physics