A uniform beam of mass M = 5 kg and length L = 2 m is attached at one end to a wall via a hinge. The other end is supported by a rope so that the beam makes a 30° angle with the vertical (see diagram). The angle between the rope and the beam is 90°.

a) What is the tension in the cable?

b) What is the force that the hinge exerts on the beam?

a) This is clearly a statics problem, with the beam as our object of interest. The forces on it are its weight, the tension in the rope (T), and the hinge force. Choose x=horizontal, y=vertical. Break the unknown force at the hinge into horizontal F_H and vertical F_V components. Consider torques about the hinge point:

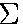
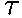= 0 = Mg(L/2)sin - TL

where we have chosen clockwise as the positive direction. Thus,

T = (Mg/2)sin

   = (5 kg)(9.8 m/s2/2)sin(30°)

   = 12.25 N

b) Now consider the forces: In the x-direction we have

F_H - Tcos = 0

or

F_H = Tcos = (12.25 N)cos(30°) = 10.61 N

In the y-direction we have

F_V + Tsin - Mg = 0

F_V = Mg - Tsin

   = (5kg)(9.8 m/s²) - (12.25 N)sin(30°)

   = 42.88 N

Thus the hinge force is

10.61 N i + 42.88 N j

Next problem
Test 3 page
Physics 101 Home page
Physics Department Home Page