A bicycle wheel starts off at rest. It is acted on by a constant torque for a time of 15 seconds. During this time, the wheel makes 80 revolutions.

a) What is magnitude of the angular acceleration of the wheel?

b) Assume that the torque was created by a force F = (6N i + 5N j) acting at a displacement of r = (2m i - 3m j) from the axle of the wheel. Calculate the torque vector.

c) Given the results from a) and b), what is the moment of inertia of the bicycle wheel (about its axle)?

a) Constant torque implies constant angular acceleration. Therefore we can use our 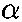=constant relations, and thus we know that the total angle turned through is given by

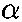= (1/2)t²

since the initial angular velocity 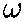₀ = 0 .

Thus we have

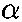= 2/t²

We convert the number of revolutions into an angle:

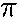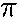= (80 rev)(2 rad/rev) = 160 rad

thus

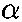= 2 (160 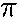rad)/(15 s)² = 4.47 rad/s²

b) Apply the cross product:

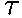= r x F = (2m i - 3m j) x (6N i + 5N j)

= 10 N·m k   +   (-18 N·m) (-k)

= 28 N·m k

where we have used   i x i = 0, i x j = +k, j x i = -k, and j x j = 0.

c) Now use 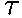= I 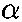to get the moment of inertia:

I =/

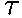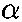
= (28 N·m)/(4.47 rad/s²) = 6.27 Kg·m²

Next problem
Test 3 page
Physics 101 Home page
Physics Department Home Page