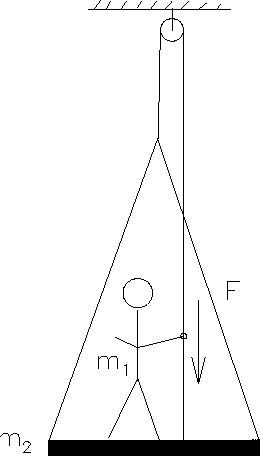A painter of mass m₁ = 60 kg stands on a platform of mass m₂ = 15 kg, which is suspended by a massless rope over a frictionless pulley as shown. She raises herself by pulling down on the rope with force F.

a) What force F is needed to keep the painter and platform moving with constant velocity?

b) Assume instead that F = 400 N (downward). What is the acceleration of the person and the platform?

Easier solution:

Since the painter and the platform move together, we can consider them together as one system of mass m₁+m₂. There are only three forces acting on this system, all of them in the vertical direction:

i)   The weight of the system = (m₁+m₂)g downward

ii)   The reaction force that the rope exerts on the painter, F. From the 3rd law, if the painter pulls down on the rope with F, the rope pulls back up on the painter with F.

iii)   The force that the other end of the rope exerts on the platform (where it is attached at the top). Since the rope is massless, the tension in the rope is uniform throughout, so this is also F upwards.

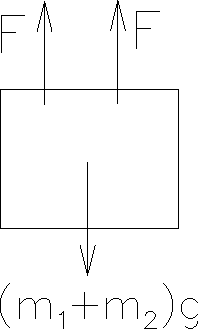
Thus, applying F = Ma to the system, and setting a=0 (since velocity is a constant), we have

F + F - (m₁+m₂)g = 0

or

F = (1/2)(m₁+m₂)g

= (1/2)(60 kg + 15 kg)(9.8 m/s²) = 368 N

b) repeat, this time where a is non-zero, but now F is fixed to be 400 N:

F + F - (m₁+m₂)g = (m₁+m₂)a

or

a = [2F - (m₁+m₂)g]/(m₁+m₂) = 0.867 m/s² (upwards)

a) There are two masses involved, m₁ and m₂, so we can draw force diagrams for each.

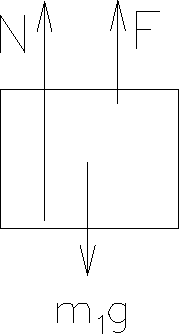
For the painter (m₁) we have the upward normal force N that the platform exerts on her, her weight (m₁g downward), and the upward force the rope exerts on her (since she pulls down on the rope, Newton's 3rd law says the rope pulls up with an equal yet opposite force on her). All the forces are vertical, so we have

F + N - m₁g = m₁a = 0        (i)

since a=0 for constant velocity.

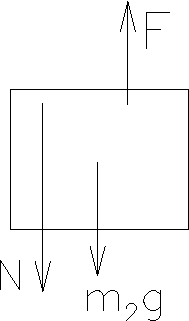
For the platform (m₂) we have the downward normal force N that the painter exerts (equal and opposite to N!), its weight (m₂g downward), and the upward force the rope exerts (after it passes over the pulley) on the top of the platform. Since the rope is massless, the tension in the rope is constant throughout, so this is just F. Again, all the forces are vertical, and again, the acceleration is required to be zero, so we have

F - N - m₂g = m₂a = 0        (ii)

So, we have two equations in two unknowns (T, and F), so the problem is solved except for the algebra. Solving (i) for N we have

N = m₁g -F

plugging this into (ii) we have

F - (m₁g - F) - m₂g = 0

or

2F = (m₁+ m₂)g

F = (1/2)(m₁+ m₂)g = (1/2)(60 kg + 15 kg)(9.8 m/s²) = 368 N

b) Everything is the same as above (same force diagrams), except now the acceleration is not zero, and the F is given. Thus we have, as above,

F + N - m₁g = m₁a       (i)

and

F - N - m₂g = m₂a       (ii)

Now we again have two equations in two unknowns (a and N), and so all we have left is algebra. From (ii) we have:

N = F - m₂a - m₂g

plugging this into (i) we get

F + (F - m₂a - m₂g) - m₁g = m₁a

2F - (m₁a + m₂)g = (m₁g + m₂)a

or

a = [2F- (m₁a + m₂)g]/(m₁g + m₂)

plugging in the masses, F=400 N, and the value of g we get

a = + 0.867 m/s²

where the positive sign indicates that the acceleration is upwards.

Next problem
Test 1 page
Physics 101 Home page
Physics Department Home Page

---

College of William and Mary,
Dept. of Physics