Problem 4:
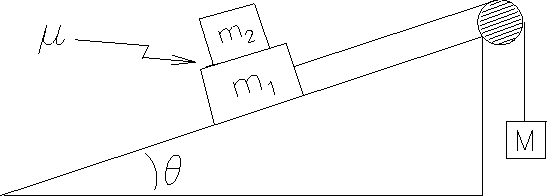 A mass M is suspended by a rope, which goes around
a pulley and is connected to mass m1 = 3 kg which
sits on an inclined plane. A mass m2 = 2 kg sits on
top of m1 , as shown. The incline angle is
A mass M is suspended by a rope, which goes around
a pulley and is connected to mass m1 = 3 kg which
sits on an inclined plane. A mass m2 = 2 kg sits on
top of m1 , as shown. The incline angle is
 = 17° .
The pulley is frictionless, the rope is massless,
and there is no friction between m1 and the incline.
However, there is friction between m1 and
m2 ,
with coefficients µs = 0.4 and µk = 0.2 .
= 17° .
The pulley is frictionless, the rope is massless,
and there is no friction between m1 and the incline.
However, there is friction between m1 and
m2 ,
with coefficients µs = 0.4 and µk = 0.2 .
a) What is M if this system is in equilibrium (i.e.
nothing is moving)?
b) What is the maximum value of M such that m2
rides on top of m1 without slipping?
Solution:
-
a) Draw force diagrams; here, since m1 and m2
are not moving, we can treat them as one object of mass =
m1 + m2. The rope is massless, so the tension
from the diagram for mass M is the same as the tension for the
mass on the incline. We have, from the hanging mass:
- T - Mg = 0
- (since we have a=0) or
- T = Mg
- and for the masses on the incline we have:
- x: T - (m1 + m2)gsin
 =
0
=
0
- y: N - (m1 + m2)gcos
 =
0
=
0
- (again, since a=0). We don't need the y-equation right now; just plug in T = Mg from
above to the x-equation to give
- Mg = (m1 + m2)gsin

- M = (m1 + m2)sin
 = (5 kg)sin(17°)
= 1.46 kg easy!
= (5 kg)sin(17°)
= 1.46 kg easy!
- b) This is a bit harder; we now have to treat m2 and m1 separately. Draw
force diagrams for each, and note that the frictional force on m1 points down the incline,
as it opposes motion, which means by the 3rd law, the frictonal force on m2 must point
up the incline (this is good, since we want to have m2 go up the incline, and so there
better be a force pointing that way!). Thus, for m2
- x: Ff -m2gsin
 = m2a
= m2a
- y: N2 - m2gcos
 = 0
= 0
- N2 = m2gcos

- We have the usual inequality for the frictional force; since we want the maximum mass M, then we
will need the maximum frictional force, so we can replace the inequality by the equality
- Ff = µsN2
- where we use the static frictional coefficient, since the two surfaces will be at rest with
respect to each other. Thus we can solve for the maximum acceleration that this maximum frictional
force can provide:
- Ff = µsN2 = µs
m2gcos

- hence
- µs
m2gcos
 - m2gsin
- m2gsin = m2a
= m2a
- a = µsgcos
 - gsin
- gsin
- For M we have
- T - Mg = Ma
- or
- T = M(g+a)
- Finally, for the two-mass system, we have
- T - (m1 + m2)gsin
 =
(m1 + m2)a
=
(m1 + m2)a
- similar to part a), except here a is non-zero. Plug in T = M(g+a), rearrange, and
plug in
a = µsgcos
 - gsin
- gsin to get
to get
- M(g+a) = (m1 + m2)(a + gsin
 )
)
- M(g+µsgcos
 - gsin
- gsin ) =
(m1 + m2)(µsgcos
) =
(m1 + m2)(µsgcos - gsin
- gsin + gsin
+ gsin )
)
- M = (m1 + m2)(µscos
 )/(1+µscos
)/(1+µscos +µscos
+µscos )
)
- plug in the values for the masses,
 , and µs
to get
, and µs
to get
- M = 2.10 kg
Test 1 page
Physics 101 Home page
Physics Department Home Page
College of William and Mary,
Dept. of Physics
 A mass M is suspended by a rope, which goes around
a pulley and is connected to mass m1 = 3 kg which
sits on an inclined plane. A mass m2 = 2 kg sits on
top of m1 , as shown. The incline angle is
A mass M is suspended by a rope, which goes around
a pulley and is connected to mass m1 = 3 kg which
sits on an inclined plane. A mass m2 = 2 kg sits on
top of m1 , as shown. The incline angle is
 A mass M is suspended by a rope, which goes around
a pulley and is connected to mass m1 = 3 kg which
sits on an inclined plane. A mass m2 = 2 kg sits on
top of m1 , as shown. The incline angle is
A mass M is suspended by a rope, which goes around
a pulley and is connected to mass m1 = 3 kg which
sits on an inclined plane. A mass m2 = 2 kg sits on
top of m1 , as shown. The incline angle is
![]() = 17° .
The pulley is frictionless, the rope is massless,
and there is no friction between m1 and the incline.
However, there is friction between m1 and
m2 ,
with coefficients µs = 0.4 and µk = 0.2 .
= 17° .
The pulley is frictionless, the rope is massless,
and there is no friction between m1 and the incline.
However, there is friction between m1 and
m2 ,
with coefficients µs = 0.4 and µk = 0.2 .