Problem 2:
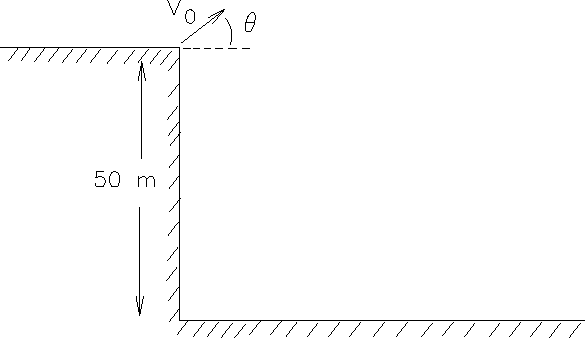 Tiger Woods hits a golf ball off
the edge of a 50 m high cliff, at an initial
speed of 30 m/s and an initial angle
Tiger Woods hits a golf ball off
the edge of a 50 m high cliff, at an initial
speed of 30 m/s and an initial angle
 = 40° from the horizontal.
Neglect air resistance.
= 40° from the horizontal.
Neglect air resistance.
a) How long is the ball in flight?
b) How far from the base of the cliff does
it land?
c) What is the ball's speed just before it hits the ground?
Solution:
-
This is clearly a projectile motion problem. We won't be able to
use the `Range' equation for part b), since the initial and final
heights differ, so we better just start at the beginning.
- Choose a coordinate system with y=vertical, x=horizontal, and
the origin at the base of the cliff.
- The equation for the y-component is
- y = y0 + v0yt + ½at2
- Now put in the condition that it reach the ground (y=0), call
the height of the cliff y0, set a = -g, and
v0y = v0sin
 . Then the equation is
. Then the equation is -
- 0 = y0 + v0sin
 t
- ½gt2
t
- ½gt2 -
- which is a quadratic equation for t. Plugging in the values
v0 = 30 m/s, g = 9.8 m/s2,
 = 40°, and solving we get the two solutions
= 40°, and solving we get the two solutions
- t = -1.79 s t = +5.71 s
- The first is unphysical (it is before the ball was hit - even Tiger Woods
isn't that good!), so we choose
the second solution: The ball was in flight for
5.71 s.
- b) Now that we know the flight time, we can plug it into the
x-equation:
- x = x0 + v0xt
-
- where x0=0 here, and v0x =
v0cos
 , so
, so
- x = (30 m/s)cos(40°)(5.71 s) = 131 m
- c) The x-component of the velocity is a constant (no horizontal acceleration),
and so
- vx = vox = v0cos
 = (30 m/s)cos(40°) = 23.0 m/s
= (30 m/s)cos(40°) = 23.0 m/s
- The y-component of the velocity is
- vy = v0y - g t
- = (30 m/s)sin(40°) - (9.8 m/s2)(5.71 s)
- = -36.8 m/s
- The speed is then
- v = [vx2 + vy2]1/2
- = [(23.0 m/s)2 + (-36.8 m/s)2]1/2
- = 43.3 m/s
Note: Part c) could also be done using energy conservation, but
that subject wasn't part of the material this test covered... Also, Tiger could have hit
it much farther, I'm sure, but the hole was located exactly where the ball landed...
Next problem
Test 1 page
Physics 101 Home page
Physics Department Home Page
College of William and Mary,
Dept. of Physics
 Tiger Woods hits a golf ball off
the edge of a 50 m high cliff, at an initial
speed of 30 m/s and an initial angle
Tiger Woods hits a golf ball off
the edge of a 50 m high cliff, at an initial
speed of 30 m/s and an initial angle
 Tiger Woods hits a golf ball off
the edge of a 50 m high cliff, at an initial
speed of 30 m/s and an initial angle
Tiger Woods hits a golf ball off
the edge of a 50 m high cliff, at an initial
speed of 30 m/s and an initial angle
![]() = 40° from the horizontal.
Neglect air resistance.
= 40° from the horizontal.
Neglect air resistance.