3) 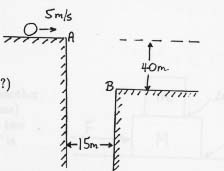Wile Y. Coyote (or is it the Roadrunner?) is running toward a deep canyon at 5 m/s and goes over the edge at A. The canyon is 15 m wide and its opposite edge is 40 m lower than A. Use g = 10 m/s².

This is clearly an example of projectile motion. We know the initial conditions, but we know only that he either lands at a specific x-value or a specific y-value, but not which one. So, we need to guess one, and see if it is correct.

Let's guess that he lands on the ground beyond B. Now, choose our coordinate system. I chose (x,y) = (0,0) as the point A, x is positive to the right and y is positive upwards. The equations of motion are (no acceleration in the x-direction!):

x = x₀ + v_0xt

and

y = y₀ + v_0yt + ½at²

where   x₀=0,   y₀=0,   v_0x = 5 m/s,   v_0y = 0 m/s,   and a = -10 m/s²

Setting y = -40 m (the location of the ground beyond B) the y-equation gives

- 40 m = ½(- 10 m/s²)t²

solving this gives

t = 2.83 s

Now, we need to find if this is sufficient time to have reached the other side of the canyon. We apply the x-equation

x = (5 m/s)(2.83 s) = 14.1 m

which is less than the canyon's 15 m width. Ouch - we guessed wrong, and he must instead hit the canyon wall somewhere below B. Clearly it must by the Coyote, since the Roadrunner never misses a jump....

To find out where he hits, we apply the projectile motion equations again, but this time with the final   x   known to be 15 m:

x = 15 m = v_0xt

or

t = x/v_0x = 15 m/(5 m/s) = 3 s

stick this into the y-equation to see how far he has fallen by that time:

y = ½(- 10 m/s²)(3 s)²

= - 45 m

This is

  (-40 m) - (-45 m) =   5 m   below point B