Problem 4:

4) 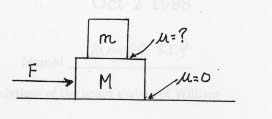A box of mass m is sitting on top of another box of mass M, which sits on a (frictionless) layer of ice. There is friction between the two boxes. A horizontal force of magnitude F is applied to the lower box (see diagram).

a) Assume that the static friction is such that the two boxes move together. What is the acceleration of the system?

b) what is the minimum coefficient of static friction between the two boxes such that they move together?

c) Now, assume that something is exerting an addtional vertical (downwards) force F₂ on the upper box. What would now be the minimum coefficient of static friction such that the boxes move together?

Solution:

a) This is very similar to one of the homework problems. If the two masses move together, we can consider them as one system of mass (m + M); we have

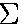F = (m + M)a

or

a = F/(m+M)

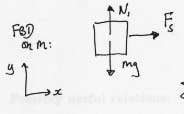
b) The frictional force is the force that causes the upper mass to have acceleration a. Draw a force diagram for this mass, with the coordinate system shown:

Apply 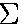  F = ma

to this mass:

x-component:   F_s = m a

y-component:   N - mg = 0

where N is the normal force and F_s the (static) frictional force. We have   F_s <= µ_sN,   but since we are interested in the minimum coefficient we can set   F_s = µ_sN. The y-equation gives

N = mg

and so the x-equation gives

F_s = µ_sN = µ_smg = ma

or, solving for µ,

µ = a/g = F/[g(m+M)]

where we have substituted in the result from a).

c) The force diagram is now: :

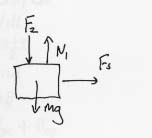Everything proceeds the same as in part b), with one additional force:

x-component:   F_s = m a

y-component:   N - mg - F₂= 0

The y-equation gives

N = mg + F₂

and so the x-equation gives

F_s = µ_sN = µ_s(mg + F₂) = ma

or, solving for µ,

µ = ma/(mg+F₂) = mF/[(mg+F₂)(m+M)]

The required frictional coefficient is reduced, since we have increased the normal force.

Test 1
Physics 101 Home page
Physics Department Home Page

---

College of William and Mary,
Dept. of Physics

armd@physics.wm.edu

last updated: Oct 2 1998