2) A yo-yo of mass m = 0.030 kg on a (massless) string of length L= 1.0 m is swung in a circular manner as shown in the sketch (gravity acts in the downward direction). The radius of the orbit is R = 0.70 m.

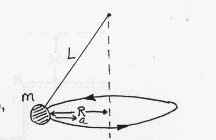
a) How long does it take the yo-yo to make one revolution (i.e. what is its period?)

b) What is the magnitude of the acceleration of the yo-yo? Indicate the direction of the acceleration at some instant in time on the sketch.

This was done as a demonstration in class; the solution is in your lecture notes from Sept. 21.

Draw a free-body force diagram for the yo-yo:

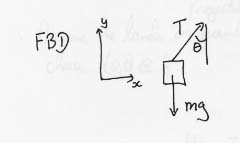
There are only two forces, the weight (mg) and the tension (F) in the string. Apply 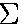  F = ma   and we get

x-component: Fsin = ma = mv²/R

y-component: Fcos - mg = 0

where we have recognized that   a=v²/R   for circular motion. Let's solve for the velocity, since we can get the period using   v = 2R/T. From the y-component equation we have

F = mg/cos

substitute into the x-equation to get

mgsin/cos = mv²/R

rearrange this to get

v = [Rgtan]^1/2

thus the period is

T = 2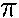R/[Rgtan]^1/2

Now, using   sin = R/L   we have

= sin^-1(R/L)

= sin^-1(70/100)

= 44.4°

thus

T = 2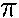(0.7 m)/[(0.7 m)(9.8 m/s²)tan(44.4°)]^1/2

= 1.70 s

b) We use   a = v²/R   and our relation given above for v to get the acceleration

a = (Rgtan)/R = gtan = 9.61 m/s²

The direction of a is radially inward (this is what the word "centripetal" means) is. Notice that the acceleration in this case is nearly as large as g; one could predict this since the angle is almost 45°....

Next Problem
Test 1
Physics 101 Home page
Physics Department Home Page