Eugene R. Tracy
Professor of Physics and Director of Graduate House
P.O. Box 8795
College of William and Mary
Williamsburg, VA 23187-8795
tracy@physics.wm.edu
ph.(757)221-3527; fax (757)221-3540
My vita (last updated March, 1999) (PDF
format)
Research interests: Plasma theory and
nonlinear dynamics
I am most interested in dynamics, i.e. the study of how things change.
I am particularly interested in the development of new tools which will
help us to peer more deeply and with more subtlety into the dynamical behavior
of physical systems. I have done work on soliton theory, turbulence,
signal processing, and short wavelength asymptotics. Much, but not all,
of this work has dealt with nonlinear phenomena. My present research interests
fall into two broad categories:
Nonlinear dynamics
The current emphasis of my work in nonlinear dynamics concerns the
analysis of signals from nonlinear systems. One major area of effort
concerns the use of symbolic methods to analyze signals. In
this approach the signal is severely coarse grained and converted into
a long string of just a few symbols (for example, '0' and '1'). The
statistical properties of this symbol string are then analyzed for multi-step
correlations. Such an approach to the analysis of signals is appealing
because: 1] it is robust to noise, and 2] it involves
only counting in binary and is, hence, very fast computationally.
Previous work by our group and others have shown that the symblic data
alone is often sufficient for solving many of the standard problems in
signal analysis: estimation of characteristic timescales, detection
of periodicities, and the testing and validation of models. Our current
interests concern the detection of symbolic precursors of instabilities.
Here the dynamics of the system is weakly non-stationary in time.
The symbolic data is sampled in moving windows and the statistical properties
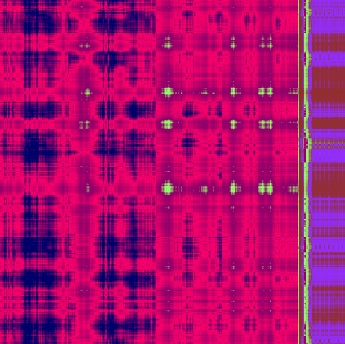
of the symbols in different windows is compared. In the figure at
right we show a cross correlation plot comparing the symbolic behavior
of a dynamical system with the noise driving it. The system eventually
undergoes what is called a subcritical Hopf bifurcation (thought
to occur, for example, in turbines and other machines). Early times are
at the upper left and later times at the lower right. The instability
occurs along the right edge. What should be noticed is the shifting
pattern of color (implying changing statistical behavior) as one moves
to the right (toward the instability).
Phase space analysis of wave propagation in
non-uniform media
This topic (also known as ray tracing or WKB analysis) has a long history
in mathematical physics, dating all the way back to the original work of
Hamilton who first derived his famous equations in the context of wave
optics in nonuniform media. Short wavelength asymptotics has become a well-developed
area of mathematical physics and applications can be found in all branches
of physics. My efforts in this area have concentrated on situations where
the WKB approximation breaks down. This work is carried out in collaboration
with Prof. Allan N. Kaufman of UC Berkeley and the plasma theory group
at Lawrence Berkeley National Lab.
For example: Non-uniform plasmas can support many different types of
waves and in some situations there can be regions where two or more waves
become "degenerate" (both local dispersion relations are satisfied simultaneously).
This is a resonance phenomena, much like the coupling of two oscillators,
and it leads to a significant exchange of energy, momentum, and action
between the various wave modes. In these degenerate regions the WKB method
fails and a local approximation must be used. We have recently developed
a general set of analytical tools which cast these problems into a canonical
form for which a general solution can be found. 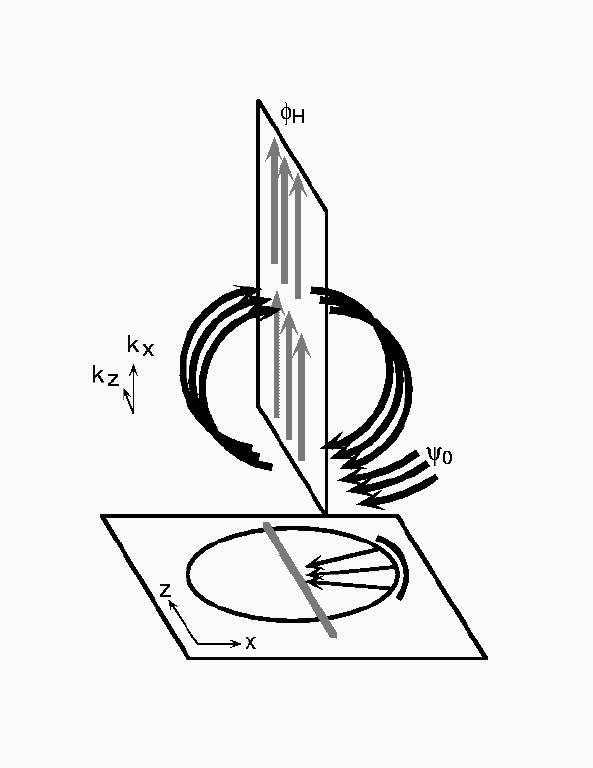 We
are extending these techniques to include sources in order to study the
emission of radiation by particles in nonuniform media, a basic problem
which is still open. The firgure at right shows a phase space diagram for
a ray analysis of RF heating in a tokamak. This involves launching
electromagnetic (magnetosonic) rays from an antenna, propagating them into
the plasma and through resonance with another mode (the ion-hybrid).
As this resonance is crossed, some of the energy of the incoming waves
is converted to the ion-hybrid, and some transimitted through the resonance.
Because the magnetosonic rays are confined they bounce at the edge of
the plasma and can re-enter the resonance. This can occur ad infinitum
with
the energy gradually leaking into the ion-hybrid mode and propagating to
high wavenumbers, where it generates fine scale spatial structure in the
plasma which is damped by other processes. We have also recently applied
these techniques to the study of equatorial wave dynamics in the ocean.
We
are extending these techniques to include sources in order to study the
emission of radiation by particles in nonuniform media, a basic problem
which is still open. The firgure at right shows a phase space diagram for
a ray analysis of RF heating in a tokamak. This involves launching
electromagnetic (magnetosonic) rays from an antenna, propagating them into
the plasma and through resonance with another mode (the ion-hybrid).
As this resonance is crossed, some of the energy of the incoming waves
is converted to the ion-hybrid, and some transimitted through the resonance.
Because the magnetosonic rays are confined they bounce at the edge of
the plasma and can re-enter the resonance. This can occur ad infinitum
with
the energy gradually leaking into the ion-hybrid mode and propagating to
high wavenumbers, where it generates fine scale spatial structure in the
plasma which is damped by other processes. We have also recently applied
these techniques to the study of equatorial wave dynamics in the ocean.
I have active collaborations with the plasma theory group at UC Berkeley
and the nonlinear ocean wave group at the University of Torino in Italy.
The work is supported by the Department of Energy, Office of Fusion Energy
and the Air Force Office of Scientific Research, Program on Dynamics and
Control.
Recent talks and publications
Other activities: The
Graduate Center at William & Mary
Last updated March 29, 1999

 We
are extending these techniques to include sources in order to study the
emission of radiation by particles in nonuniform media, a basic problem
which is still open. The firgure at right shows a phase space diagram for
a ray analysis of RF heating in a tokamak. This involves launching
electromagnetic (magnetosonic) rays from an antenna, propagating them into
the plasma and through resonance with another mode (the ion-hybrid).
As this resonance is crossed, some of the energy of the incoming waves
is converted to the ion-hybrid, and some transimitted through the resonance.
Because the magnetosonic rays are confined they bounce at the edge of
the plasma and can re-enter the resonance. This can occur ad infinitum
with
the energy gradually leaking into the ion-hybrid mode and propagating to
high wavenumbers, where it generates fine scale spatial structure in the
plasma which is damped by other processes. We have also recently applied
these techniques to the study of equatorial wave dynamics in the ocean.
We
are extending these techniques to include sources in order to study the
emission of radiation by particles in nonuniform media, a basic problem
which is still open. The firgure at right shows a phase space diagram for
a ray analysis of RF heating in a tokamak. This involves launching
electromagnetic (magnetosonic) rays from an antenna, propagating them into
the plasma and through resonance with another mode (the ion-hybrid).
As this resonance is crossed, some of the energy of the incoming waves
is converted to the ion-hybrid, and some transimitted through the resonance.
Because the magnetosonic rays are confined they bounce at the edge of
the plasma and can re-enter the resonance. This can occur ad infinitum
with
the energy gradually leaking into the ion-hybrid mode and propagating to
high wavenumbers, where it generates fine scale spatial structure in the
plasma which is damped by other processes. We have also recently applied
these techniques to the study of equatorial wave dynamics in the ocean.