|
Slow and Stored Light in Atomic Vapor
My research program is focused on the manipulation
of light pulse propagation through an atomic vapor and the development of efficient
memory for a photon quantum state, and aimed to find the optimal operation conditions
for practical realization of quantum information algorithms. The results of these
experiments can be used later for better understanding of more complex systems (e.g.
quantum dots or doped crystals).
The light storage technique, described above, is capable of transferring quantum states of light to atomic ensembles and back perfectly only under the condition of no dissipative optical losses and no decay of atomic quantum states. In realistic systems various loss mechanisms reduce the fidelity of the storage. Several research groups have already reported proof-of-principle experiments demonstrating essential tools for quantum networks, such as on-demand single photon generation and storage of a single photon in atomic ensemble. However, the efficiency and fidelity of these operations are still very low and must be improved dramatically before they can be used for practical applications. 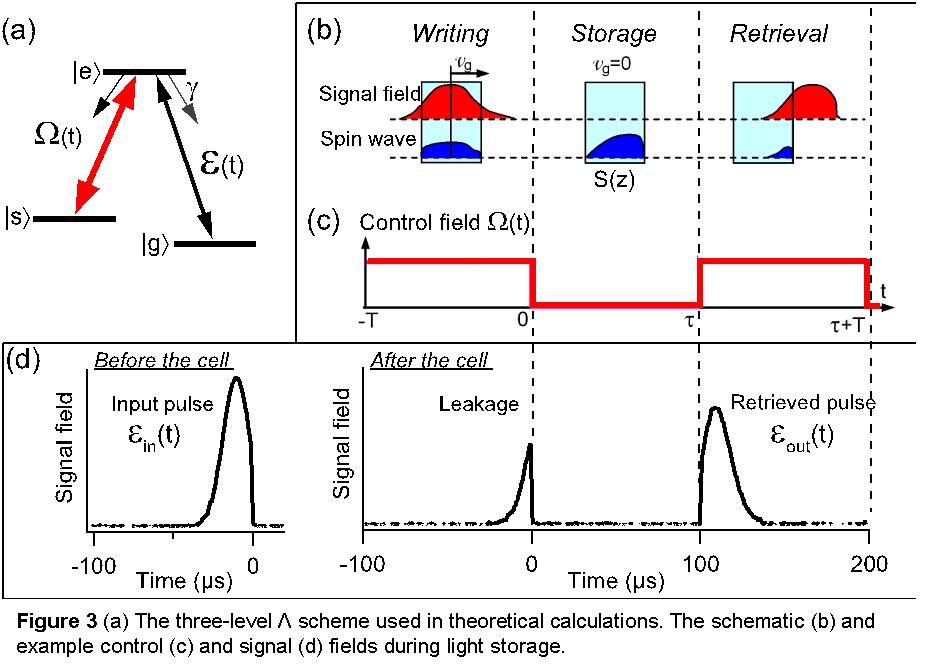
We consider the propagation of a weak signal pulse with envelope E(t) and a strong, classical control field with Rabi frequency envelope Ω(t) in a resonant Λ-type atomic medium under conditions of EIT, as depicted in Fig. 3a. Each Λ-type atom possesses two long-lived electronic ground states, |g› and |s›, and a single excited state, |e›, as in sub-levels of different angular momentum within the electronic ground state of alkali atoms. For our experiments, light fields were tuned near the 87Rb D1 (λ=795 nm) transition. States |g› and |s› corresponded to |F, mF›=|1, 1›, |2, 1›, respectively; |e› corresponded to |F’, mF’›=|2, 2›. The control field
creates a strong coupling between the signal field and a collective atomic spin
excitation (spin wave). The two fields collaborate to place an atom into a
coherent superposition of the two ground states, which no longer interacts with
the optical fields. For a narrow range of signal field frequencies near the
two-photon resonance, the previously-opaque medium is rendered transparent. The
width of this so-called EIT window is determined by
the strength of the control field,
where γ is the optical polarization decay rate and α is the absorption coefficient, so that αL is the optical depth of an atomic medium of length L. Accompanying this anomaly in the signal field’s transmission spectrum is a very steep, linear change in the refractive index, resulting in a dramatically reduced group velocity for the signal pulse,
Since vg depends on the control field’s
intensity, pulse propagation through an EIT medium
can be used as the basis for quantum memory. Figure 3(b) illustrates the three
stages of the light storage process (writing, storage, and retrieval), while Figs.
3(c) and 3(d) show control and signal fields, respectively, during a typical
experimental run. At the writing stage, a signal pulse Ein(t) is
mapped onto spin wave S(z) by adiabatically reducing the control field (and
hence vg) to zero. This spin wave is then preserved for some
storage time τ, during which all optical fields are turned off.
Lastly, the signal field Eout(t) is retrieved by re-illuminating the control field. We characterize the memory by computing the storage efficiency as
the probability of retrieving an incoming photon after storage, or
equivalently, as the energy ratio between initial and retrieved signal pulses.
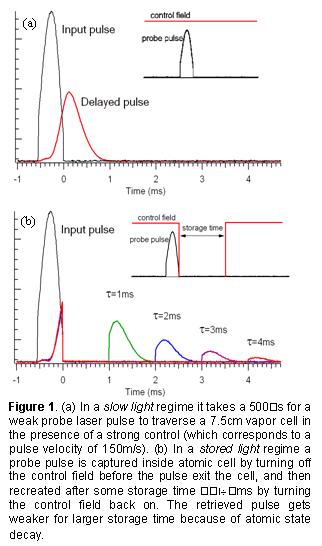
To realize ideal storage (and optimize efficiency), two conditions must be met.
On one hand, vg must be low enough to spatially compress the
whole pulse of duration T into the length of the ensemble and avoid
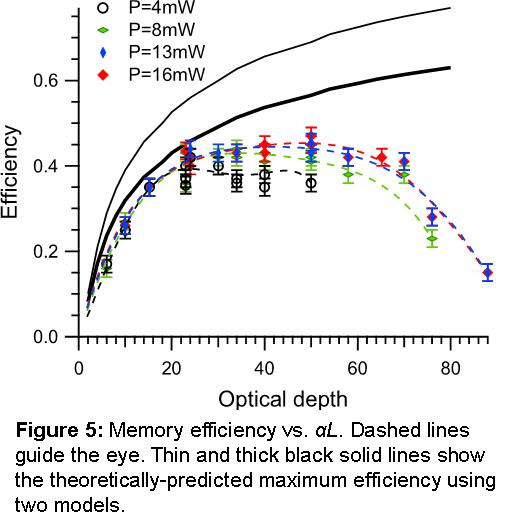
"leaking" the front edge of the pulse past the atoms ( In order to improve the memory efficiency, it is necessary to operate at high optical depth (high Rb concentration). We performed iterative optimization over a range of optical depths, as shown in Fig. 5. We clearly see that for optical depths up to αL=25, efficiency grows as theoretically predicted. Between αL=25 and 60, efficiency levels off; we suspected this was due to resonant FWM, discussed next. Above αL=60, storage efficiency degrades because unprepared atoms absorb the control field.
In order to understand the effects of FWM on light storage, we performed experiments in the cw, slow-, and stored-light regimes wherein we seeded the FWM process by sending an input Stokes field (in addition to input signal and control fields) into the vapor cell. We were able to adjust the relative amplitudes of the input signal and Stokes fields. We
developed a theoretical model of the EIT-FWM
interaction, which accurately describes experimental observations and provides
an intuitive understanding of light storage under FWM
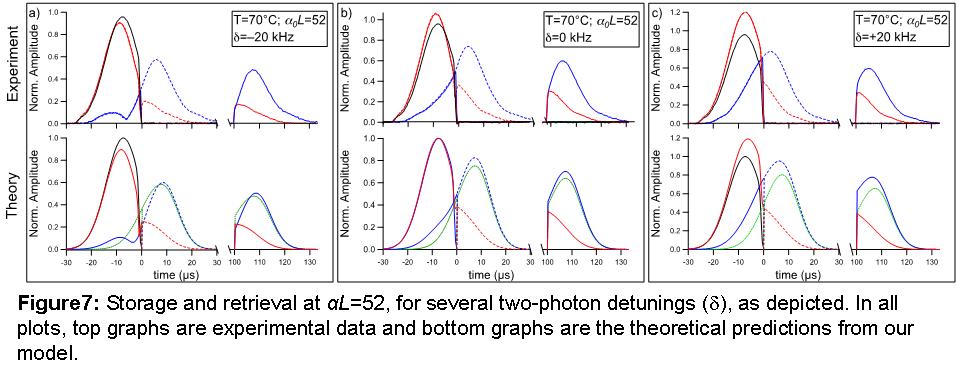
conditions. Figure 7 shows the results of storage experiments under EIT-FWM conditions and demonstrates the effectiveness of
our model.
|
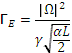
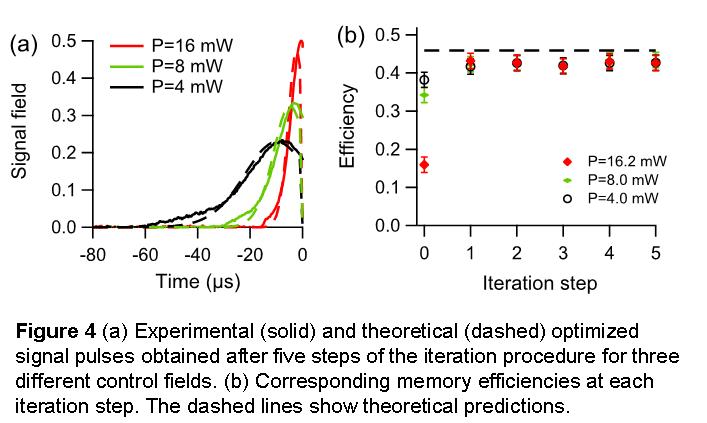
 We have demonstrated the efficacy of two memory optimization
protocols. The first is based on the time-reversal symmetry of the storage
process, which we exploit to iteratively determine an optimally-stored signal
pulse for a given control field
We have demonstrated the efficacy of two memory optimization
protocols. The first is based on the time-reversal symmetry of the storage
process, which we exploit to iteratively determine an optimally-stored signal
pulse for a given control field 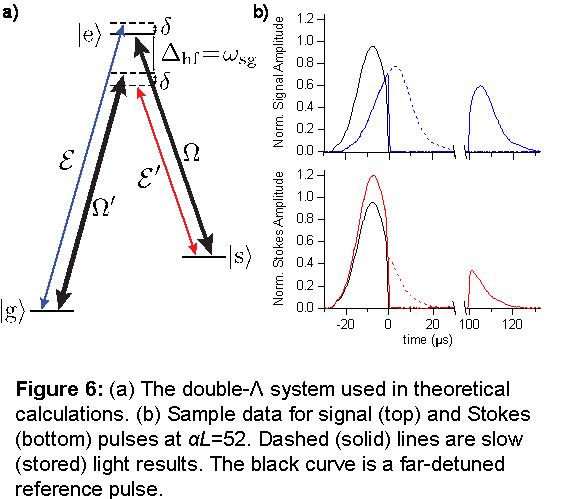 For low optical depths, it is sufficient to take into account only
the effects of the single-Λ. However, due to resonant
For low optical depths, it is sufficient to take into account only
the effects of the single-Λ. However, due to resonant