In the following experiment, the class listened to a series of 20 pairs of broad-band noise samples. The first in the pair was the reference sound and the second was stronger or weaker in intensity. The reference was assigned a value of 100. Students were asked to assign a 'loudness' value [ 0 = inaudible; 100 = same as reference; 200 = twice as loud as the reference; 50 = half as loud as the reference, etc.] to the second sound of each pair.
Such a subjective scale may vary from person to person and trial to trial for the same person. However, on average, a consistent pattern emerges.
The data are arranged in rows of 20 values, one for each sample. Each row is a different trial; pairs of rows correspond to the same person repeating the experiment. The sound intensity levels, compared to the reference tone (0dB) were:
+15,-5,-20,0,-10,+20,+5,+10,-15,0,-10,+15,+20,-5,+10,-15,-5,-20,+5,+15
The recorded values for each intensity level were averaged to produce the following table:
The columns are: 1) relative sound intensity level in dB 2) average loudness value assigned by the class 3) standard deviation of the assigned loudness 4) standard error of the assigned loudness 5) actual sound intensity in W/m^2, assuming a reference tone of 80 dB. -20 32.8286 25.0992 2.99993 1.0e-6 -15 41.1571 17.206 2.05651 3.2e-6 -10 57.5571 18.349 2.19312 1.0e-5 -5 79.7714 19.6988 1.92241 3.2e-5 0 96.2714 13.1126 1.56725 1.0e-4 5 128.557 21.2921 2.54489 3.2e-4 10 158.971 29.2664 3.498 1.0e-3 15 224.352 37.5576 3.66525 3.2e-3 20 276.371 35.4614 4.23845 1.0e-2

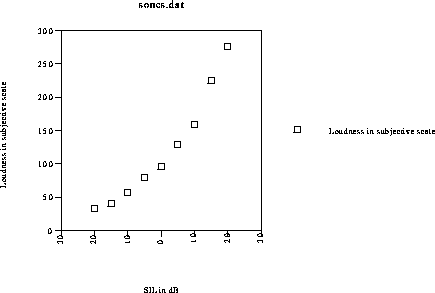
Figure 1. The average subjective loudness value versus the relative sound intensity level in dB. If the data fell on a straight line they would indicate that humans hear the powers of ten in intensity (i.e. dB) rather than intensity itself. Since the data do not exactly fall on a straight line, we may be able to find a slightly better model.
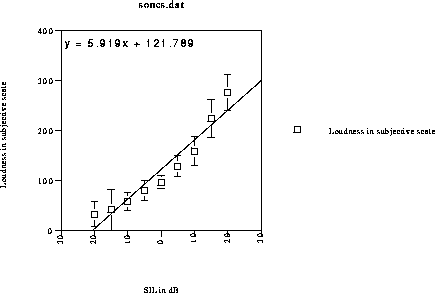
Figure 2. Subjective loudness versus relative sound intensity level in dB, fit to a straight line. The errors are the standard deviation of the values at each loudness level. That is, they measure the width of the bell curve for the class's answers. Properly, however, the error in the average value is not this standard deviation, but the standard error, which is smaller than the size of the points.
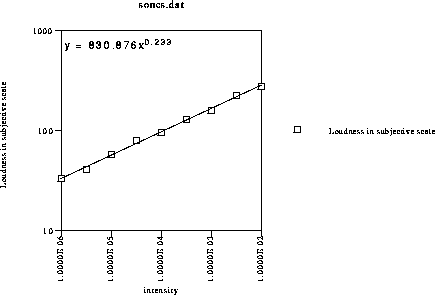
Figure 3. The average subjective loudness ratings versus sound intensity in watts per square meter. The plot is a log-log plot. In other words, each power of 10 is a fixed length along the axis. The data fall very nicely on a straight line. This indicates that perception of loudness varies as a power of the intensity. The best-fitting relationship is
0.23
Loudness (sones) = Constant x Intensity
In other words, perceived loudness varies roughly as the 4th root of the sound
intensity.