A speed skier (mass = 90 kg) starts at rest from the top of a 125 m high hill. Assume that the ski slope is frictionless until point B, after which there is a coefficient of kinetic friction µ_k = 0.25. The ground is level i.e. the height is constant) to the right of point B. Ignore air resistance everywhere.

a) What is his speed at point B?

b) How far from point B does he finally come to rest?

c) What is the total work done by friction?

a) We can apply conservation of energy to the first part of his trip (up until point B), since there are no non-conservative forces (friction, drag) for this part. Choose the zero of gravitational potential to be the height of the level portion. Thus we have

E = mgh + ½mv_A² = mg(0) + ½mv_B²

or, since v_A = 0,

mgh = ½mv_B²

v_B = [2gh]^1/2 = [2(9.8 m/s²)(125 m)]]^1/2 = 49.5 m/s

b) He will come to rest because of friction; thus the total work done by the non-conservative force (friction) must be the total change in mechanical energy i.e.

W_friction = 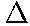E = 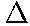K = 0 - ½mv_B²

   = - ½(90 kg)(49.5 m/s)² = 110 kJ

The frictional force is constant, and given by µ_k times the normal force = mg, so we also have that the work done by friction is

W_friction = F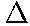x = µ_kmg 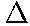x

or

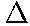x = W_friction/( µ_kmg)

= (110 kJ)/[0.25)(90 kg)(9.8 m/s²)] = 500 m

Aside: An even more elegant solution is to equate the W_friction directly to the initial energy  = mgh to get

mgh = µ_kmg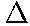x

or

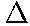x = h/µ_k = 500 m

c) We have already worked out the work (oops, apologies for the pun) above, so we have

W_friction = 110 kJ

Test 2 page
Physics 101 Home page
Physics Department Home Page