Problem 1:
A 4 kg mass is attached to a spring which has a spring constant
of 16 N/m. The spring is stretched to 5.0 cm from the equilibrium
position, and released (starting with zero initial velocity).
Assume there is no friction or damping. For the resulting oscillation,
find the:
- a) amplitude
- b) period
- c) maximum speed of the mass
- d) magnitude of the maximum acceleration of the mass
- e) position of the mass after 2 seconds
- f) the general equation of motion, i.e. x(t)
Solution:
a) By definition of the amplitude, it is 5.0 cm (or 0.05 m).
b) 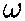 = [k/m]1/2 =
[(16 N/m)/(4kg)]1/2 = 2 rad/s
T = 2
= [k/m]1/2 =
[(16 N/m)/(4kg)]1/2 = 2 rad/s
T = 2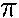 /
/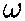 =
= 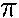 seconds
seconds
c) The general equation for SHM is
x(t) = A cos( 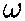 t +
t +
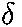 )
so can get the speed from
dx/dt = -A
)
so can get the speed from
dx/dt = -A 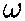 sin (
sin ( 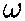 t +
t + 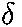 )
and thus the maximum speed is
vmax = A
)
and thus the maximum speed is
vmax = A 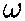 = (0.05 m)(2 rad/s) = 0.10 m/s
= (0.05 m)(2 rad/s) = 0.10 m/s
d) Similarly, the maximum acceleration is
amax = A 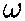 2
= (0.05 m)(2 rad/s)2 = 0.20 m/s2
2
= (0.05 m)(2 rad/s)2 = 0.20 m/s2
e) We have x = A cos( 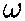 t +
t +
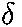 ), where here
), where here 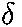 =0, since the function is at its maximum at time t=0
(starting at rest, with maximum stretch). Plugging in t = 2s,
we have
x(t=2s) = (0.05 m) cos [(2 rad/s)(2 s)] = -0.033 m
=0, since the function is at its maximum at time t=0
(starting at rest, with maximum stretch). Plugging in t = 2s,
we have
x(t=2s) = (0.05 m) cos [(2 rad/s)(2 s)] = -0.033 m
f) The general equation of motion is
x = (0.05m) cos[(2 rad/s)t]
Next problem
1998 Test 3 page
Physics 101 Home page
Physics Department Home Page
College of William and Mary,
Dept. of Physics
armd@physics.wm.edu
last updated: Nov. 23 1998