Problem 4:
-
4) A toy car of mass M slides (not rolls) down a
frictionless track that makes a circular loop of
radius R at the bottom. The car starts from rest
at height H, where H > 2R.
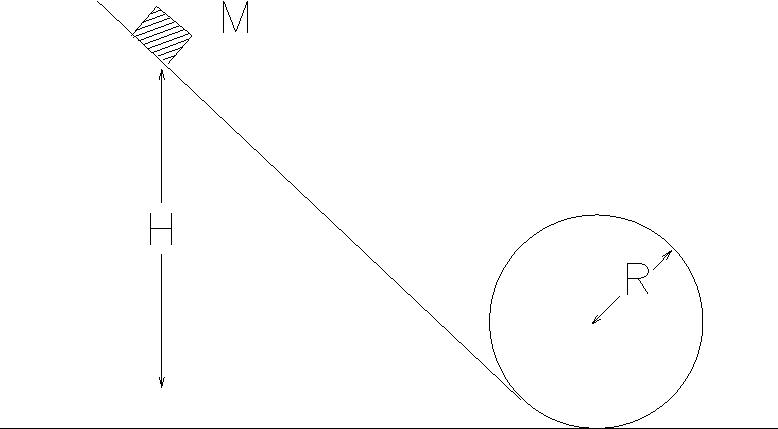
- a) What is the car's speed at the bottom of the circle?
- b) What is the car's speed at the top of the circle?
- c) What is the minimum value of H such that the car goes
around the loop without falling off under the force of gravity?
Solution:
-
a) We apply conservation of energy to the slide of the car down the
frictionless track (as all the forces are conservative here). Choosing
the zero of gravitational energy to be at the bottom of the circle,
and noting that the car starts off with zero kinetic energy we have:
- Einitial = Efinal
- 0 + MgH = (1/2) Mv2 + 0
- thus
- v = (2gH)1/2
- b) Again, apply conservation of energy:
- MgH = (1/2) Mv2 + Mg(2R)
- since the height at the top is twice the radius. Rearranging,
we get
- v2 = 2gH - 4gR
- v = (g[2H-2r])1/2
- c) Now to find whether it goes around the loop, we need to consider
forces; if one draws a force diagram for the mass when it is at the top
of the loop, there are only two forces acting on it, both vertically
downward: Mg and N (the normal force provided by the track). Thus we have
- N + Mg = Mv2/R
- the limiting case is N=0 (i.e. since N cannot be negative, so
for any lower starting height, i.e. lower velocity, we cannot
satisfy the equation, and thus it cannot continue in the circle, and
falls off), so we have
- v2 = gR
- now applying energy conservation, for starting at a new height
Hnew, we have
-
MgHnew = (1/2)Mv2 + Mg(2R)
- substituting in for v2 we get
-
MgHnew = (1/2)M(gR) + Mg(2R)
- or, dividing out Mg,
-
Hnew = (1/2)R + 2R = (5/2)R
Test 2
Physics 101 Home page
Physics Department Home Page
College of William and Mary,
Dept. of Physics
armd@physics.wm.edu
last updated: Oct 26 1998
