Problem 4:
A merry-go-round of radius 2 m is rotating about a frictionless pivot.
It makes one revolution every 5 s. The moment of inertia of the
merry-go-round (about an axis through its center) is
500 kg·m2.
A child of mass 25 kg, originally standing at the rim, walks in
to the exact center. The child can be considered as a point mass.
-
a) What is the new angular velocity of the merry-go-round?
- b) Does the total kinetic energy of the system increase or
decrease? By how much?
- c) Where does this change in energy go to or come from?
Solution:
-
a) This is just like problem 10-49, except this time the child
starts at the outside and walks inward instead of vice-versa.
Apply conservation of angular momentum (there are no net external torques
on the system of merry-go-round and child). Thus we have
- L = constant = Ii
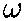 i =
If
i =
If
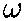 f
f
- or
-
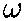 f =
Ii
f =
Ii
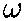 i/ If
i/ If
-
- so all that is left to do is to find the initial angular velocity
and the initial and final moments of inertia. We are told the period
(T = 5 seconds) so the initial angular velocity is
-
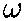 i = 2
i = 2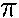 /T = 1.257 rad/s
/T = 1.257 rad/s
- The initial moment-of-inertia is that of the merry-go-round plus that
of the child located at the rim
- Ii = 500 Kg·m2 + mR2
-
- = 500 Kg·m2 + (25 kg)(2 m)2
- = 600 kg·m2
- Since the child ends up at the center (r=0), she/he contributes
no rotational inertia in the final situation, so the If
is just that of the merry-go-round, i.e.
-
- If = 500 Kg·m2
-
- Plugging these in gives
-
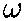 f =
(600 kg·m2)(1.257 rad/s)/(500 Kg·m2)
f =
(600 kg·m2)(1.257 rad/s)/(500 Kg·m2)
- = 1.51 rad/sec
- b) The initial rotational kinetic energy is
- Ki = ½Ii
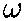 i2
i2
- = ½(600 kg·m2)(1.257 rad/s)2
- = 474 J
- the final rotational kinetic energy is
- Kf = ½If
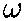 f2
f2
- = ½(500 kg·m2)(1.51 rad/s)2
- = 568 J
- Thus the energy has increased by 94 J.
- c) The extra energy had to have come from somewhere, in this case
from stored (chemical) energy in the child's muscles - the child did work on the merry-go-round while walking in to the center.
Test 3 page
Physics 101 Home page
Physics Department Home Page
College of William and Mary,
Dept. of Physics
armd@physics.wm.edu
last updated: Nov. 23 1998