A uniform beam of mass M and length L is attached at one end to a wall via a hinge. The other end is supported by a horizontal cable so that the beam makes an angle with the vertical (see diagram).

a) What is the tension in the cable?

b) What is the force that the hinge exerts on the beam?

c) The cable snaps; what is the initial angular acceleration of the beam (about the hinge point)? The moment of inertia of a uniform bar about an axis through one end is 1/3 ML²

This is problem 11-39, one of the suggested extra problems. It should be clear that this is [at least until part c)], a typical statics problem.

a) We draw a force diagram for the beam, with coordinate system x=horizontal and y=vertical, as shown.

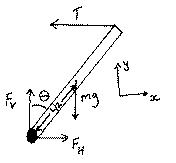
The only forces acting on it are the tension T, the weight Mg, and the force exerted by the hinge, which for convenience we can break into vertical and horizontal components, F_V and F_H, respectively.

Now we write F = 0 and = 0 using the force diagram:

x-component of forces: F_H - T = 0

y-component of forces: F_V - Mg = 0

and we take torques about an axis through the hinge point (so that the equation does not involve the hinge forces, and so is particularly simple):

TLcos - Mg(L/2)sin = 0

where we have used the fact that the moment arm for the tension is Lcos and that for the weight is (L/2)sin. Solving this last equation for the tension gives

T = ½Mgtan

b) The force equations give us directly the hinge force:

F_V = Mg

F_H = T = ½Mgtan

thus

F_hinge = ½Mgtan i + Mg j

c) If the cable snaps, there is no more tension, and thus there is an unbalanced torque due to gravity. Since = I we have

Mg(L/2)sin = I = (1/3)ML²

or

= Mg(L/2)sin/ (1/3)ML² = 3gsin/2L

The direction of this torque is into the page (-k) since it causes a rotation in the clockwise sense. Notice that the torque will change in magnitude as the bar falls (since will change), so the angular acceleration will not be a constant...