Physics 101 - Homework # 6 Solutions
Note: Symbols written in Bold are vectors.
Chapter 8
Problem 28)
- The 241Am nucleus is at rest before emitting the
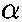 particle,
so the
particle,
so the 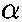 particle and 237Np nucleus must move in opposite
directions, which makes this a one-dimensional situation.
particle and 237Np nucleus must move in opposite
directions, which makes this a one-dimensional situation.
- a) Because momentum is conserved, we can write
- mAmvAm =
m
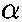 v
v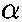 + mNpvNp
+ mNpvNp
- 0 = (4m0)v
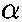 + (237m0)vNp
+ (237m0)vNp
- which gives
- vNp = -(4/237)v
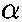
- The released energy (=Q) must be the kinetic energies of the emitted
products (subtle point: this assumes that the particles are
emitted in their ground states rather than in excited states):
- Q = ½m
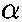 v
v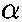 2 +
½mNpvNp2
2 +
½mNpvNp2
- 9.6 x 10-13 J = ½(4m0)v
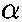 2 +
½(237m0)(4/237)2v
2 +
½(237m0)(4/237)2v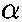 2
2
- = 2.034m0v
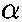 2
2
- where m0 = 1.66 x 10-27 kg
; thus
- v
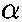 = 1.70 x 107 m/s
= 1.70 x 107 m/s
- vNp = 2.85 x 105 m/s
- b) The kinetic energies are
- K
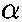 = ½(4)(1.66 x 10-27 kg)(1.70 x 107
m/s2)2 =
9.58 x 10-13 J
= ½(4)(1.66 x 10-27 kg)(1.70 x 107
m/s2)2 =
9.58 x 10-13 J
- KNp = ½(237)(1.66 x 10-27 kg)(2.85 x 105
m/s2)2 = 1.59 x 10-14 J
- Almost all the energy is carried off by the lighter product (the
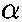 particle).
particle).
Problem 32)
-
a) Because momentum is conserved, we can write
- m1v1 + m2v2
= m1v3 + m2v4
- (0.30 kg)(1.4 m/s)i + (0.15 kg)(-2.5 m/s)i =
(0.30 kg)v3i + (0.15 kg)v4i
- Because the collision is elastic, the relative velocity does not change:
- v1 - v2 =
- (v3 - v4)
- or
- (1.4 m/s) i - [ - (2.5 m/s)i] = - (v3i -
v4i)
- Combining these two equations, we get, after a bit of algebra,
- v3 = - 1.2 m/s and
v4 = 2.7 m/s
- The total initial kinetic energy is
- Ki = ½m1v12 +
½m2v22
- = ½(0.30 kg)(1.4 m/s)2 +
½(0.15 kg)(-2.5 m/s)2 = 0.76 J
Problem 43)
- For the collision of the two masses, we use momentum conservation:
- mv + 0 = mv1 + mv2
- (2.50 m/s)i = [(0.50 m/s)i + ( -1.00 m/s)j]
+ v2
- which gives
- v2 = (2.00 m/s)i + (1.00 m/s)j
-
- To test whether the collision is elastic, we find the kinetic energy
before and after:
- Ki = ½m(2.50 m/s)2 = (3.13 m) J
- Kf = ½m[ (0.50 m/s)2 + (-1.00 m/s)2
+ (2.00 m/s)2 + (-1.00 m/s)2 ] = (3.13 m) J
- These are equal no matter what m is.
Because the kinetic energy is conserved, the collision is elastic.
- Since the masses are the same, we could also show that the final
velocities are perpendicular
- v1·v2 =
[(0.50 m/s)i + (-1.00 m/s)j]·[(2.00 m/s)i
+ (1.00 m/s)j] = 0
- since that is also true only ff the collision was elastic (see text,
Eq 8-44).
Problem 49)
- We use momentum conservation for the collision; consider the
x and y-components separately:
- x-direction:
- mcarvcar,i + 0 =
mcarvcar,fcos
 car +
mtruckvtruck,fcos
car +
mtruckvtruck,fcos truck
truck
- (1000 kg)vcar,i = (1000 kg)vcar,fcos60°
+ (1500 kg)(21.6 m/s)cos33.7°
- y-direction:
- 0 + 0 = -mcarvcar,fsin
 car
+ mtruckvtruck,fsin
car
+ mtruckvtruck,fsin truck
truck
- 0 = -(1000 kg)vcar,fsin60° +
(1500 kg)(21.6 m/s)sin33.7°
- These are two equations in two unknowns; solving, we get
- vcar,f = 20.8 m/s and vcar,i
= 37.4 m/s = 84 mi/h.
- The driver of the car was speeding (unless they were driving down the
Autobahn...).
Problem 52)
- We find the center of mass from (the sums run over i)
- R =
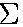 mri/
mri/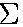 mi
mi
- = [(0.2 kg)0 + (0.1 kg)(0.3 m)j + (0.3 kg){(0.2 m)i
+ (0.2 m)j}]/(0.2 kg + 0.1 kg + 0.3 kg)
- = (0.10 m)i + (0.15 m)j
Problem 57)
- We ignore the size of the iron block, and treat it as a point mass.
The center of mass of the handle will be at its midpoint, from symmetry
arguments. We choose the
origin at the bottom of the handle. For the system, we have
- X =
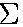 mixi/
mixi/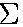 mi
mi
- = [(4.0 kg)(0) + (1.8 kg)(0)]/(4.0 kg + 1.8 kg) =
0 m
- Y =
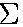 miyi/
miyi/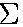 mi
mi
- = [(4.0 kg)(1.2 m) + (1.8 kg)(0.6 m)]/(4.0 kg + 1.8 kg) = 1.0 m
from the bottom of the handle.
Problem 73)
-
We choose the positive direction to be the original direction of motion,
which we take to be to the right. The center-of-mass velocity is found from
(see Eq. 8-50 in the text, for example):
-
a) vCM = (m1v1 +
m2v2)/(m1 + m2)
- = [(48 kg)(6 m/s) + (82 kg)(9 m/s)]/(48 kg + 82 kg) =
7.9 m/s (to the right)
-
b) Because there are no outside (or external) forces, the velocity of the center of mass
will not change:
- vCM = 7.9 m/s (to the right)
- We can show this explictly by calculating the new velocity of the
pair after they collide using conservation of momentum, and then
calculating vCM similarly to what was done in part a).
-
c) The center of mass frame is a reference frame moving with the velocity of
the center-of-mass; in this reference frame, we have
- v1' = v1 - vCM = 6 m/s - 7.9 m/s =
- 1.9 m/s (to the left)
- v2' = v2 - vCM = 9 m/s - 7.9 m/s =
+ 1.1 m/s (to the right)
-
d) We find the average force on the skaters from the momentum change
(the impulse):
- J = Fav
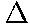 t =
t =
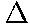 p
p
- Fav =
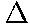 p/
p/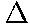 t = (48 kg + 82 kg)(0 - 7.9 m/s)/(0.05 s)
= -2.1 x 104 (to the left)
t = (48 kg + 82 kg)(0 - 7.9 m/s)/(0.05 s)
= -2.1 x 104 (to the left)
- Therefore, the force on the barrier is the reaction to this force:
- 2.1 x 104 N (to the right)
- The momentum of the two-skater system is not conserved any more since
in the collision with the barrier there is now a net external force
(caused by the barrier).
Problem 75)
- a)
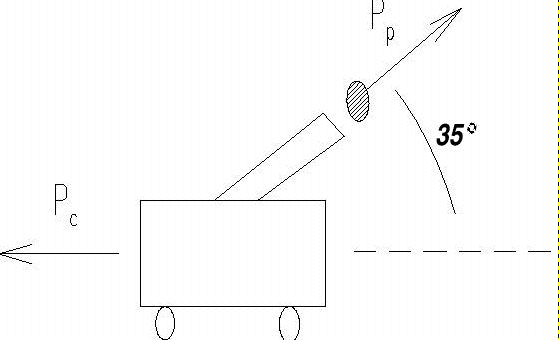
- b) In the horizontal direction, momentum is conserved:
- 0 = pproj cos35° - pcannon
- 0 = (5 kg)(800 m/s)cos35° - (800 kg)vcannon
- which gives the cannon's recoil velocity as
- vcannon = 4.1 m/s
- along the ground.
- c) The recoiling cannon's component of momentum perpendicular to the ground remains
zero because of the upward impulse provided by the ground; the earth
therefore recoils
(infinitesimally) downwards, conserving the total vertical component of momentum.
Problem 78)
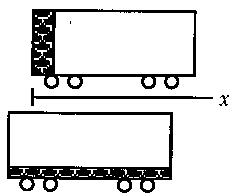
- We choose the boxcar and the water as a system, with the origin at
the end of the boxcar with the tank. Because there are no horizontal
external forces, the horizontal momentum will stay=zero always, and the
center of mass of the system will not move horizontally. We can find
the center of mass, before the tank leaks, from
- X =
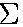 mixi/
mixi/
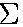 mi
mi
- = {2400 kg)(0.5 m) + (3200 kg)(4 m)]/[2400 kg + 3200 kg] = 2.5 m
- After the tank empties, mass is distributed uniformly, so the
center of mass must be X' = 4.0 m from the end. Because the center of
mass does not move, the boxcar must move X'-X = 1.5 m
toward the end where the water was.
Physics
101 Solutions
Physics
101 Home page
Physics Department Home
Page
College of William and Mary
Dept. of Physics
armd@physics.wm.edu
last updated: Sept. 6 2000
