Physics 101 - Homework # 1 Solutions

• Problem 1-3
• Problem 1-8
• Problem 1-10
• Problem 1-23
• Problem 2-1
• Problem 2-6
• Problem 2-15
• Problem 2-17
• Problem 2-32
• Problem 2-35
• Problem 2-42
• Problem 2-56

Chapter 1

Problem 3)

Cube root = (10²¹)^1/3 = 10^21/3 = 10⁷
Square = (10⁷)² = 10¹⁴

Problem 8)

Price = (1.90 DM/L)($1/1.7 DM)(3.8 L/gal) = $4.25/gal

Problem 10)

This is a unit conversion problem [note the typo in the question; dimensional analysis tells us that the units of G to convert to must be cm³s^-2g^-1 not cm³s²g^-1, since the dimensions are L³T^-2M^-1 ]. Convert by multiplying successively by "1":

G = 6.67 x 10^-11 m³s^-2kg^-1 (100 cm/1 m)³(kg/1000 g)

= 6.67 x 10^-8 cm³s^-2g^-1

(note that the factor of 100 from m to cm gets cubed... we will discuss G further later in the course... )

Problem 23)

Dimensional Analysis: For   L = h/m_ec   we can write the dimensions as

[L] = [h][m_e]^-1[c]^-1
      = [h][M]^-1([L][T]^-1)^-1

thus

[h] = [L][M] [L][T]^-1 = [ML²T^-1]

      (thus in SI units h would be in kg m²/s; h is known as Planck's constant, and is central in Quantum mechanics...)

Chapter 2

Problem 1)

The net displacement is the sum of each individual displacement:

= + 32 cm - 27 cm - 23 cm + 39 cm = +21 cm

Since the initial position in this case was the origin, the grasshopper is 21 cm from the origin in the positive direction.

Problem 6)

This can be solved graphically using a plot of distance vs. time

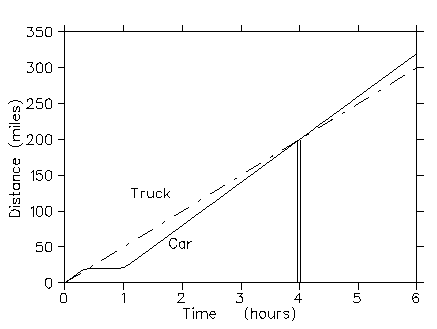
The two curves intersect at time t=4 hours, i.e. the car and truck meet again 4 hours after the initial passing.

Problem 15)

From   x = 0.02t³ - 0.1t² + 2 t   cm    we get the speed via

v = dx/dt = 0.06t² - 0.2t + 2 cm/s.

Then

v₁ = 0.06(1)² - 0.2(1) + 2 = + 1.86 cm/s;    v₁ = + 1.86 cm/s

v₅ = 0.06(5)² - 0.2(5) + 2 = + 2.5 cm/s;    v₅ = + 2.5i cm/s

v₁₀ = 0.06(10)² - 0.2(10) + 2 = + 6.0 cm/s;    v₁₀ = + 6.0 cm/s

The magnitude of the average velocity is    v_av = x/t

Problem 17)

We are told that the acceleration is a constant here, a = 0.6 m/s² so we have

v = v₀ + at

Rearranging, we have

t = (v-v₀₎/a

The final velocity is v = 40 mi/hr; we assume that the car starts at rest, so v₀ = 0, and so we have (converting units along the way):

t = (40 mi/hr)(1 hr/3600 s)(1.609 x 10³m/mi)/(0.6 m/s²)

= 29.8 s

Problem 32)

For constant acceleration, the average speed is just ½(v₀ + v); thus

x = v_avt = ½(v₀+v)t

x = ½(0 + 4.2 x10³ mi/h)(125 s)(1h/3600 s)

which gives   x = 73 mi

Problem 35)

a)

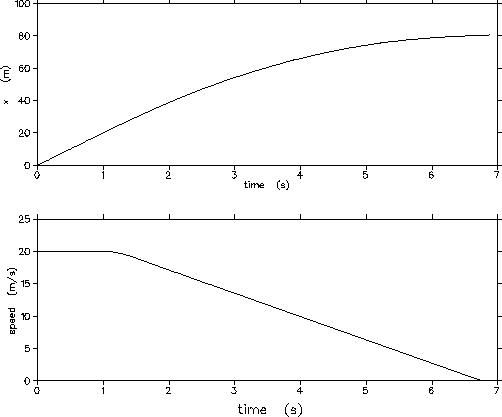
b) We can first find the distance travelled before the brakes were applied using

x₁ = v₀t₁ = (20 m/s)(1.2 s) = 24 m

We can then find the acceleration while the brakes were applied using

v² = v₀² + 2 a (x₂ - x₁)

thus

0 = (20 m/s)² + 2 a (80 m - 24 m)

solving for a gives

a = - 3.57 m/s²

Problem 42)

With the origin chosen at the point where the brakes are applied, we have v₀ = 40 mi/h = 58.7 ft/s    and   a = 0.5 g   where   g = 32 ft/s². We can find the distance she travels before stopping from

v² = v₀² + 2a(x-x₀)

0 = (58.7 ft/s)² + 2 [(-0.5(32 ft/s²)](x-0)

which gives

x = 107 ft

Because this is greater than 100 ft, she does not stop before arriving at the light.

Problem 56)

Let's choose a coordinate system with the origin at the release point, and with downwards being positive (why should up always be positive?). This is motion under constant acceleration, so we have

x = x₀ + v₀t + (1/2)at²

Substituting in the values x₀ = 0 m, x = 10 m (the ground), v₀ = 0, and a = 25.9 m/s², we have

10 m = 0 + 0 + (1/2)(25.9 m/s²)t²

which yields

t = ± 0.88 s

We take the positive root (can you see why?) to give

t = 0.88 s